题目内容
20.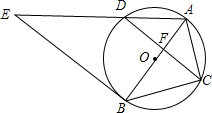 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.求证:直线BE是⊙O的切线.
分析 先利用垂径定理得到$\widehat{AD}$=$\widehat{AC}$,则∠ACD=∠ADC,再证明CD∥BE,则利用平行线的性质得到AB⊥BE,然后根据切线的判定定理可判断直线BE是⊙O的切线.
解答 证明:∵CD⊥AB,
∴$\widehat{AD}$=$\widehat{AC}$,
∴∠ACD=∠ADC,
∵∠E=∠ACF,
∴∠E=∠ADC,
∴CD∥BE,
∴AB⊥BE,
∴直线BE是⊙O的切线.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理、圆周角定理.

练习册系列答案
相关题目
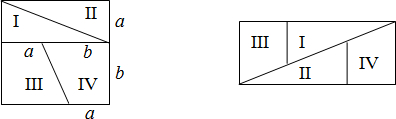
10.如图,将左边正方形剪成四块,恰能拼成右边的矩形,若a=2,则b的值是( )

| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{3}$+1 |
8.下列方程中是一元一次方程的是( )
| A. | 4x-5=0 | B. | 2x-y=3 | C. | 3x2-14=2 | D. | $\frac{1}{x}$-2=3 |
9.把8.32°用度、分、秒表示正确的是( )
| A. | 8°3′2″ | B. | 8°30′20″ | C. | 8°19′12″ | D. | 8°18′12″ |