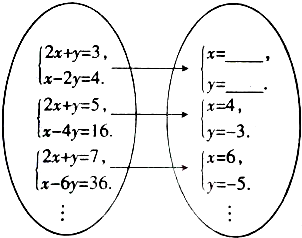
题目内容
甲、乙两个工程队.甲单独完成工作需20天,甲队每天费用5万元.乙单独完成工作需30天,乙队每天费用3万元.若要求完成这项任务的费用不超过95万元,问怎样设计甲、乙两个队的工作时间,才能使工作时间最短?
考点:一元一次不等式的应用
专题:
分析:由题意可知:要使使工作时间最短,甲队要干的天数最多,设甲队干x天,则乙队需要干(1-
)÷
=30-
x天,根据完成这项任务的费用不超过95万元列出不等式求得答案即可.
| x |
| 20 |
| 1 |
| 30 |
| 3 |
| 2 |
解答:解:设甲队干x天,则乙队需要干(1-
)÷
=30-
x天,由题意得
5x+3(30-
x)≤95
解得:x≤10,
∵要使使工作时间最短,甲队要干的天数最多,
∴x=10,
则30-
x=15.
答:甲队干10天,乙队需要干15天.
| x |
| 20 |
| 1 |
| 30 |
| 3 |
| 2 |
5x+3(30-
| 3 |
| 2 |
解得:x≤10,
∵要使使工作时间最短,甲队要干的天数最多,
∴x=10,
则30-
| 3 |
| 2 |
答:甲队干10天,乙队需要干15天.
点评:此题考查一元一次不等式的实际运用,理解题意,找出题目不等关系,列出不等式解决问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
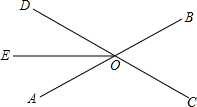 如图,直线AB,CD相交于点O,OE平分∠AOD,∠BOC=∠BOD-30°,求∠COE的度数.
如图,直线AB,CD相交于点O,OE平分∠AOD,∠BOC=∠BOD-30°,求∠COE的度数.