题目内容
若一元二次方程x2-3x+2a=0的两个实数根是x1，x2，且x1=2x2，求a的值．
考点：根与系数的关系
专题：
分析：由一元二次方程x2-3x+2a=0的两个实数根是x1，x2，得出x1+x2=3，x1x2=2a，进一步利用x1=2x2，求得两根的值，代入求得a的值即可．
解答：解：∵x1，x2是关于x的一元二次方程x2-3x+2a=0的两个实数根，
∴x1+x2=3，x1x2=2a，
∵x1=2x2，
∴x1=2，x2=1，
∴2a=2，
则a=1．
∴x1+x2=3，x1x2=2a，
∵x1=2x2，
∴x1=2，x2=1，
∴2a=2，
则a=1．
点评：此题考查一元二次方程根与系数的关系：x1+x2=-
，x1x2=
．
| b |
| a |
| c |
| a |
练习册系列答案
相关题目
如图，△AOB中，∠O=90°，AB=5cm，OA=4cm．
已知OE是∠BOC的平分线，且∠AOE=90°，∠AOC=110°，则∠BOC=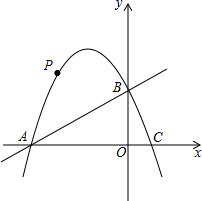
在平面直角坐标系中，直线y=x+4与x、y轴分别交于A、B两点，抛物线y=-x2+bx+c经过A、B两点，并与x轴交于另一点C（点C在点A的右侧），点P是抛物线上的一个动点．