题目内容
1．
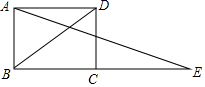如图，BD为矩形ABCD的一条对角线，延长BC至E，使CE=BD，连接AE．若AB=1，∠AEB=15°，求BD的长度．
分析 由矩形的性质和已知条件得出CE=CA，得出∠AEB=∠CAE=15°，求出∠ACB=∠AEB+∠CAE=30°，由直角三角形的性质得出AC=2AB=2，即可得出BD=AC=2．
解答 解：连接AC，如图所示：
∵四边形ABCD是矩形，
∴AC=BD，∠ABC=90°，
∵BD=CE，
∴CE=CA，
∴∠AEB=∠CAE=15°，
∴∠ACB=∠AEB+∠CAE=30°，
∴AC=2AB=2，
∴BD=AC=2．
点评 本题主要考查矩形性质、等腰三角形的性质、直角三角形的性质、三角形的外角性质，熟练掌握矩形的性质和直角三角形的性质是解题关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB=66°，则∠AED′的度数为48°．
如图所示．在?ABCD中，E为BC上一点，且AD=DE，AE、DC的延长线交于点F，∠ADE=30°，求∠CEF的度数．
16．
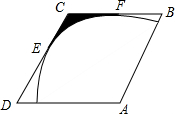如图，菱形ABCD的边长为2，∠A=120°，以点A为圆心的圆弧与菱形ABCD的DC，BC两边相切，切点分别为点E、F，则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π．
如图，菱形ABCD的边长为2，∠A=120°，以点A为圆心的圆弧与菱形ABCD的DC，BC两边相切，切点分别为点E、F，则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π． 
如图，O是矩形ABCD对角线的交点，BO=BE，∠AOD=120°，∠AEO=30°．
13．
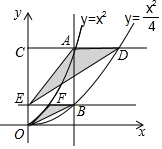如图，垂直于x轴的直线AB分别与抛物线C1：y=x2（x≥0）和抛物线C2：y=$\frac{{x}^{2}}{4}$（x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E，F，则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为（ ）
如图，垂直于x轴的直线AB分别与抛物线C1：y=x2（x≥0）和抛物线C2：y=$\frac{{x}^{2}}{4}$（x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E，F，则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为（ ）| A． | $\frac{\sqrt{2}}{6}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
10．若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2k≤0}\\{x+k＞2}\end{array}\right.$有解，则k的取值范围为（ ）
| A． | k＞-$\frac{2}{3}$ | B． | k＞$\frac{2}{3}$ | C． | k≤$\frac{2}{3}$ | D． | k≥-$\frac{2}{3}$ |