题目内容
16.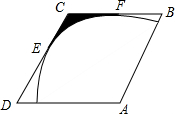 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
分析 根据S阴=2•S△ACE-S扇形AEF,只要求出AE,∠EAF的值即可解决问题.
解答 解:如图连接AE、AF、AC.
∵四边形ABCD是菱形,∠A=120°,
∴AD=AB=BC=CD=AC=2,
∠DCA=∠ACF=60°,
∵CD、BC是切线,
∴AE⊥CD,AF⊥BC,
∴AE=AF=AD•cos30°=$\sqrt{3}$,DE=$\frac{1}{2}$AD=1,
∴CE=CF=1,
∴S阴=2•S△ACE-S扇形AEF=2×$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{60•π•(\sqrt{3})^{2}}{360}$=$\sqrt{3}$-$\frac{1}{2}$π.
故答案为$\sqrt{3}$-$\frac{1}{2}$π.
点评 本题考查切线的性质、菱形的性质、扇形的面积公式等知识,解题的关键是学会添加常用辅助线,求出圆心角和半径是突破点,属于中考常考题型.

练习册系列答案
相关题目
4.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=7}\\{nx-my=1}\end{array}\right.$的解,则$\root{3}{m+3n}$的值为( )
| A. | 3 | B. | 8 | C. | 2 | D. | $\sqrt{2}$ |
6.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
| A. | 120° | B. | 80° | C. | 60° | D. | 40° |
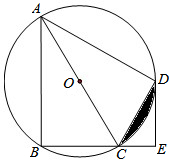 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E. 如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=20°,则∠2=110°.
如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=20°,则∠2=110°.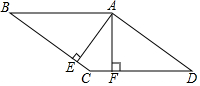 已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.
已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.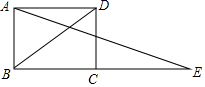 如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.
如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.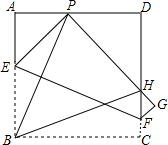 如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.
如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.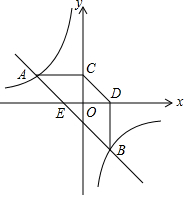 如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.
如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.