题目内容
12．
如图所示．在?ABCD中，E为BC上一点，且AD=DE，AE、DC的延长线交于点F，∠ADE=30°，求∠CEF的度数．
分析 由AD=DE且∠ADE=30°知∠DAE=75°，再根据四边形ABCD是平行四边形得AD∥BC，即可知∠CEF=∠DAE=75°．
解答 解：∵AD=DE，且∠ADE=30°，
∴∠DAE=∠AED=$\frac{180°-∠ADE}{2}$=75°，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠CEF=∠DAE=75°．
点评 本题主要考查平行四边形的性质，熟练掌握等腰三角形的性质及平行四边形的性质是解题的关键．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
相关题目
如图，在菱形ABCD中，∠BAD=135°，AB=4$\sqrt{2}$，点P是菱形ABCD内或边上的一点，且∠DAP+∠CBP=90°，连接DP，CP，则△DCP面积的最小值为8$\sqrt{2}$-8．
20．
如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2017次后，顶点A在整个旋转过程中所经过的路程之和是（ ）
如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2017次后，顶点A在整个旋转过程中所经过的路程之和是（ ）| A． | 3022.5π | B． | 3024π | C． | 3025.5π | D． | 3026π |
如图，一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上，若∠1=20°，则∠2=110°．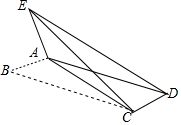
如图，在?ABCD中，AB＜BC，已知∠B=30°，AB=2$\sqrt{3}$，将△ABC沿AC翻折至△AEC，使点B的对应点E落在?ABCD所在的平面内，连接ED，若△AED是直角三角形，则BC的长为4或6．
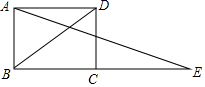如图，BD为矩形ABCD的一条对角线，延长BC至E，使CE=BD，连接AE．若AB=1，∠AEB=15°，求BD的长度．
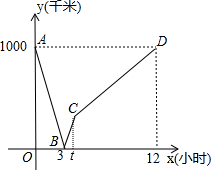首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段．宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义．试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，两车同时出发，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示y与x之间的函数关系，根据图象进行以下探究：