题目内容
13.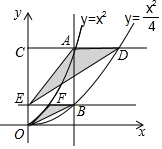 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 可以设A、B横坐标为a,易求得点E、F、D的坐标,即可求得OE、CE、AD、BF的长度,即可解题.
解答 解:设点A、B横坐标为a,则点A纵坐标为a2,点B的纵坐标为$\frac{{a}^{2}}{4}$,
∵BE∥x轴,
∴点F纵坐标为$\frac{{a}^{2}}{4}$,
∵点F是抛物线y=x2上的点,
∴点F横坐标为x=$\sqrt{y}$=$\frac{1}{2}a$,
∵CD∥x轴,∴点D纵坐标为a2,
∵点D是抛物线y=$\frac{{x}^{2}}{4}$上的点,
∴点D横坐标为x=$\sqrt{4y}$=2a,
∴AD=a,BF=$\frac{1}{2}$a,CE=$\frac{3}{4}$a2,OE=$\frac{1}{4}$a2,
∴则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$=$\frac{\frac{1}{2}BF•OE}{\frac{1}{2}AD•CE}$=$\frac{1}{8}$×$\frac{4}{3}$=$\frac{1}{6}$,
故选 D.
点评 本题考查了抛物线上点的计算,考查了三角形面积的计算,本题中求得点E、F、D的坐标是解题的关键.

练习册系列答案
相关题目
4.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=7}\\{nx-my=1}\end{array}\right.$的解,则$\root{3}{m+3n}$的值为( )
| A. | 3 | B. | 8 | C. | 2 | D. | $\sqrt{2}$ |
 如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.
如图,在菱形ABCD中,∠BAD=135°,AB=4$\sqrt{2}$,点P是菱形ABCD内或边上的一点,且∠DAP+∠CBP=90°,连接DP,CP,则△DCP面积的最小值为8$\sqrt{2}$-8.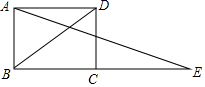 如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.
如图,BD为矩形ABCD的一条对角线,延长BC至E,使CE=BD,连接AE.若AB=1,∠AEB=15°,求BD的长度.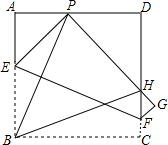 如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.
如图,现有一张边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,联结BP、BH,当AP=1时,则PH=3.4,EF=$\sqrt{17}$.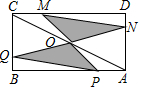 如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )
如图,矩形ABCD中,AB=8,BC=4,O为对角线AC的中点,点P,Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B,C,连接PO,QO并延长分别与CD,DA交于点M,N,在整个运动过程中,图中阴影部分面积的大小变化情况是( )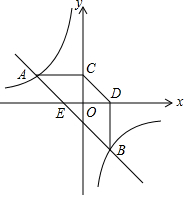 如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.
如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.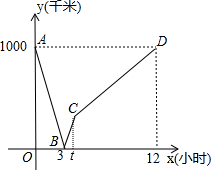 首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究:
首条贯通丝绸之路经济带的高铁线--宝兰客专进入全线拉通试验阶段.宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行以下探究: