题目内容
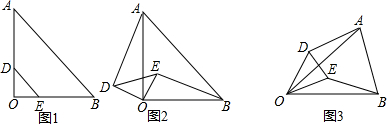
12.问题情境如图1,在△AOB与△DOE中,∠AOB=∠DOE=90°,OA=OB,OD=OE,当点D,E分别在△AOB的边OA,OB上时,结论(1)AD=BE和(2)AD⊥BE都成立.
问题探究
如图2,若当点D,E不在△AOB的边OA,OB上时,上述结论是否成立?理由.
问题延伸
如图3,将问题情境中的条件,∠AOB=∠DOE=90°换为∠AOB=∠DOE=40°,且点D,E不在△AOB的边OA,OB上时,上述结论是否成立?理由.
分析 (1)根据△AOD≌△BOE即可得到AD=BE,要证明BE⊥AD,在对顶△AKM和△BKO中利用对应角相等即可证明.
(2)利用全等三角形可以证明结论(1)成立,根据对顶△AKM和△BKO可以证明∠AMB=40°即结论不成立.
解答 (1)解:如图2中,结论仍然成立.理由如下:
延长BE交AO于K、交AD于M.
∵∠DOE=∠AOB=90°,
∴∠AOD=∠BOE,
在△AOD和△BOE中,
$\left\{\begin{array}{l}{OD=OE}\\{∠AOD=∠BOE}\\{AO=OB}\end{array}\right.$,
∴△AOD≌△BOE,
∴AD=BE,∠DAO=∠OBE,
∵∠OBE+∠OKB=90°,∠OKB=∠AKM,
∴∠DAO+∠AKM=90°,
∴∠AMK=90°,
∴BE⊥AD,BE=AD.
(2)如图3中,结论(1)AD=EB成立,结论(2)AD⊥BE不成立.
证明:∵∠AOB=∠DOE=40°,
在△AOD和△BOE中,
$\left\{\begin{array}{l}{OD=OE}\\{∠AOD=∠BOE}\\{AO=OB}\end{array}\right.$,
∴△AOD≌△BOE,
∴AD=BE,∠DAO=∠OBE,
∵∠AKM=∠OKB,
∴∠AMB=∠AOB=40°,
∴BE和AD不垂直.
点评 本题考查全等三角形的判定和性质、等角的余角相等等知识,寻找全等三角形是解决问题的关键,掌握从特殊到一般的推理方法,理解形变而结论不变的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在数轴上表示-12与-3的点的距离是( )
| A. | 15 | B. | 9 | C. | -15 | D. | 8 |
1.方程3x(x-1)=2(x-1)的解是( )
| A. | x=1 | B. | x=$\frac{2}{3}$ | C. | x1=1,x2=$\frac{2}{3}$ | D. | x1=1,x2=-$\frac{2}{3}$ |
2.方程x+2=3的解是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
 如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上.抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A.
如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上.抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A. 如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.
如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.