题目内容
1.方程3x(x-1)=2(x-1)的解是( )| A. | x=1 | B. | x=$\frac{2}{3}$ | C. | x1=1,x2=$\frac{2}{3}$ | D. | x1=1,x2=-$\frac{2}{3}$ |
分析 首先提取公因式(x-1),进而得到(x-1)(3x-2)=0,再解两个一元一次方程即可.
解答 解:∵方程3x(x-1)=2(x-1),
∴(x-1)(3x-2)=0,
∴x-1=0或3x-2=0,
∴x1=1,x2=$\frac{2}{3}$.
故选:C.
点评 本题考查了使用因式分解法解一元二次方程的知识,解此题的关键是能把一元二次方程转化成一元一次方程,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
6. 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
10.包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
| A. | 120x=2×80(42-x) | B. | 80x=120(42-x) | C. | 2×80x=120(42-x) | D. | $\frac{120(42-x)}{80x}=\frac{1}{2}$ |


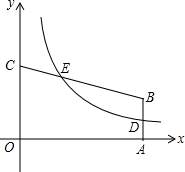 如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )
如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )