题目内容
10.如果关于x的不等(2m-n)x+m-5n>0的解集为x<$\frac{10}{7}$,试求关于x的不等式mx>n的解集.分析 解题时,要先根据已知条件找出m,并且求出m的取值范围,再解关于x的不等式mx>n即可求解.
解答 解:移项得(2m-n)x>5n-m,
∵关于x的不等(2m-n)x+m-5n>0的解集为x<$\frac{10}{7}$,
∴2m-n<0,且x<$\frac{5n-m}{2m-n}$,
∴$\frac{5n-m}{2m-n}$=$\frac{10}{7}$,
整理得n=$\frac{3}{5}$m,
把n=$\frac{3}{5}$m代入2m-n<0得,
2m-$\frac{3}{5}$m<0,解得m<0,
∵mx>n,
∴mx>$\frac{3}{5}$m,
∴x<$\frac{3}{5}$.
∴关于x的不等式mx>n的解集是x<$\frac{3}{5}$.
点评 考查了不等式的解集,注意解含字母系数的一元一次不等式要注意不等式性质3的应用,不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
20.△ABC的三边满足AC2-BC2=AB2,那么这个三角形的三个内角中( )
| A. | ∠A=90° | B. | ∠B=90° | C. | ∠C=90° | D. | 没有直角 |
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
10.包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
| A. | 120x=2×80(42-x) | B. | 80x=120(42-x) | C. | 2×80x=120(42-x) | D. | $\frac{120(42-x)}{80x}=\frac{1}{2}$ |
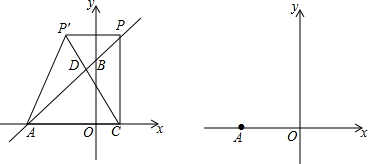
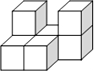 如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )