题目内容
12.在数轴上表示-12与-3的点的距离是( )| A. | 15 | B. | 9 | C. | -15 | D. | 8 |
分析 直接利用数轴上两点之间距离求法得出答案.
解答 解:在数轴上表示-12与-3的点的距离是:-3-(-12)=9.
故选:B.
点评 此题主要考查了数轴,正确掌握数轴上两点之间距离求法是解题关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
20.△ABC的三边满足AC2-BC2=AB2,那么这个三角形的三个内角中( )
| A. | ∠A=90° | B. | ∠B=90° | C. | ∠C=90° | D. | 没有直角 |
7. 已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
 已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
 如图,二次函数y=-x2-2x的图象与x轴交于点A,O,在抛物线上有一点P,满足S△AOP=3,则点P的坐标是(1,-3)或(-3,-3).
如图,二次函数y=-x2-2x的图象与x轴交于点A,O,在抛物线上有一点P,满足S△AOP=3,则点P的坐标是(1,-3)或(-3,-3).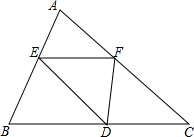 如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.
如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.