题目内容
4. 如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.
如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.
分析 首先在BE上截取BG=CF,连接OG,证明△OBG≌△OCF,则可证得△OFG是等腰直角三角形,设CE=x,利用勾股定理可得BE的长,由射影定理列方程,求得EF与CF的长,继而求得FG的长,则可求得答案.
解答 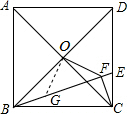 解:如图,在BE上截取BG=CF,连接OG,
解:如图,在BE上截取BG=CF,连接OG,
∵Rt△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中,
$\left\{\begin{array}{l}{OB=OC}\\{∠OBG=∠OCF}\\{BG=CF}\end{array}\right.$,
∴△OBG≌△OCF(SAS),
∴OG=OF,∠BOG=∠COF,BG=CF,
∴OG⊥OF,
设CE=x,则DE=2EC=2x,
∴BC=CD=3x,
在Rt△BCE中,
∴BE=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{10}$x,
∵EF=1,
∵CE2=EF•BE,
∴x2=$\sqrt{10}$x,
∴x=$\sqrt{10}$,
∴CE=$\sqrt{10}$,BF=BE-EF=10-1=9,
∵CF2=BF•EF=9,
∴CF=3,
∴BG=3,
∴FG=BE-BG-EF=10-3-1=6,
∴OF=$\frac{\sqrt{2}}{2}$FG=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 此题考查了正方形的性质、等腰直角三角形的性质、勾股定理以及射影定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
14.若|x|=5,|y|=3,则|x-y|等于( )
| A. | 2 | B. | ±8 | C. | 8或2 | D. | ±8或±2 |
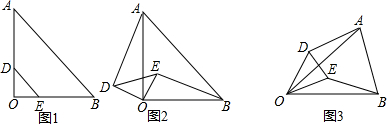
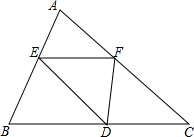 如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.
如图,△ABC中,E、F、D分别是AB、AC、BC上的点,且满足$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$,则S△ABC:S△EFD=25:6.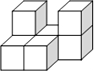 如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )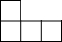



 如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:

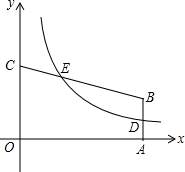 如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )
如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )