题目内容
17.已知:A=$\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$,B=$\frac{{{a^2}+{c^2}-{b^2}}}{2ac}$,C=$\frac{{{a^2}+{b^2}-{c^2}}}{2ab}$,且a+b=c,求A2013+B2013+C2013的值.分析 根据a+b=c,可以得到a、b、c之间的关系,从而可以对A=$\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$,B=$\frac{{{a^2}+{c^2}-{b^2}}}{2ac}$,C=$\frac{{{a^2}+{b^2}-{c^2}}}{2ab}$进行化简求值,进而求得A2013+B2013+C2013的值.
解答 解:∵a+b=c,
∴c-a=b,c-b=a,
∴A=$\frac{{{b^2}+{c^2}-{a^2}}}{2bc}$=$\frac{{{b^2}+(c+a)(c-a)}}{2bc}$=$\frac{{{b^2}+b(c+a)}}{2bc}$=$\frac{b+c+a}{2c}$=$\frac{2c}{2c}$=1,
B=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}=\frac{(a+b)(a-b)+{c}^{2}}{2ac}$=$\frac{c(a-b)+{c}^{2}}{2ac}=\frac{a-b+c}{2a}=\frac{2a}{2a}=1$,
C=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{{a}^{2}-(c+b)(c-b)}{2ab}$=$\frac{{a}^{2}-a(c+b)}{2ab}=\frac{a-c-b}{2b}=\frac{-2b}{2b}=-1$,
∴A2013+B2013+C2013
=12013+12013+(-1)2013
=1+1-1
=1.
点评 本题考查分式的混合运算,解题的关键是能根据a+b=c,对A、B、C进行化简求值,从而建立与A2013+B2013+C2013的关系,需要注意的是对C的化简.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
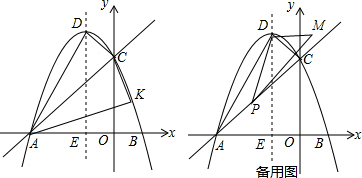
6. 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,AC与y轴交于点D,则$\frac{OD}{AD}$=( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |