题目内容
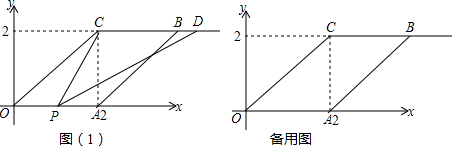
7.在平面直角坐标系中,O为原点,A为x轴正半轴上的动点,经过点A(t,0)作垂直于x轴的直线l,在直线l上取点B,点B在第一象限,AB=4,直线OB:y1=kx(k为常数).(1)当t=2时,求k的值;
(2)经过O,A两点作抛物线y2=ax(x-t)(a为常数,a>0),直线OB与抛物线的另一个交点为C.
①用含a,t的式子表示点C的横坐标;
②当t≤x≤t+4时,|y1-y2|的值随x的增大而减小;当x≥t+4时,|y1-y2|的值随x的增大而增大,求a与t的关系式并直接写出t的取值范围.
分析 (1)找出当t=2时,B点的坐标,将其代入直线OB:y1=kx中即可;
(2)①用t表示出直线OB的关系式,令y1=y2即可用含a,t的式子表示点C的横坐标;
②找出y1-y2的关系式,发现为一个开口向下的抛物线,结合给定条件能够得知,抛物线的对称轴不超过x=t,且抛物线与x轴的另一个交点为(t+4,0),由此可得出a与t的关系式并能知道t的取值范围.
解答 解:(1)当t=2时,点A的坐标为(2,0),
∵经过点A(2,0)作垂直于x轴的直线l,在直线l上取点B,点B在第一象限,AB=4,
∴点B的坐标为(2,4).
∵点B在直线OB:y1=kx(k为常数)上,
∴有4=2k,解得:k=2.
(2)①点B(t,4)在直线OB:y1=kx上,
∴有4=kt,解得:k=$\frac{4}{t}$,
∴y1=$\frac{4}{t}$x.
令y1=y2,即$\frac{4}{t}$x=ax(x-t),
解得:x=0,或者x=t+$\frac{4}{at}$.
故点C的横坐标x=t+$\frac{4}{at}$.
②y1-y2=$\frac{4}{t}$x-ax(x-t)=-ax2+(at+$\frac{4}{t}$)x.
∵a>0,
∴-a<0,函数图象开口向下,函数图象大体如下图.
∵当t≤x≤t+4时,|y1-y2|的值随x的增大而减小;当x≥t+4时,|y1-y2|的值随x的增大而增大,
∴二次函数y1-y2的对称轴在x=t的左侧或者重合,而且二次函数y1-y2与x轴的另一个交点为(t+4,0).
∵y1-y2=-ax2+(at+$\frac{4}{t}$)x=-ax(x-t-$\frac{4}{at}$),
∴有t+$\frac{4}{at}$=t+4,
解得:a=$\frac{1}{t}$.
二次函数对称轴$\frac{at+\frac{4}{t}}{2a}$≤t,即at2≥4,
∵at=1,
∴t≥4.
故当t≤x≤t+4时,|y1-y2|的值随x的增大而减小;当x≥t+4时,|y1-y2|的值随x的增大而增大时,a与t的关系式a=$\frac{1}{t}$(t≥4).
点评 本题考查了二次函数的综合应用,解题的关键是:(1)找出B点坐标代入直线OB关系式;(2)①由B点坐标表示出直线OB关系式,利用直线与抛物线交点是C可找出C点坐标;②由二次函数的图象的性质可以分析得知抛物线与x轴交点为原点和(t+4,0),结合单调性可得出t的取值范围.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案 已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )
已知:如图,正方形网格中,∠AOB如图放置,则cos∠AOB的值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
| A. | x轴的正半轴上 | B. | x轴的负半轴上 | C. | y轴的正半轴上 | D. | y轴的负半轴上 |
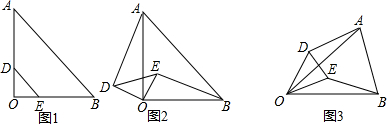
 如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.
如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.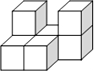 如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的俯视图是( )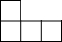



 如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论:
如图,在边长为6$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,过点C作EG的垂线CH,垂足为点H,连接BH,BH=8.有下列结论: