��Ŀ����
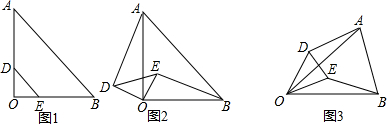
13�� ��ͼ����ƽ��ֱ������ϵ�У���CDE�Ķ���C������ΪC��1��-2������D�ĺ�����Ϊ$\frac{19}{5}$������CDE�Ƶ�C��ת����CBO����D�Ķ�Ӧ��B��x���ϣ�������y=ax2+bx+c�Ե�CΪ���㣬�Ҿ�����B������x�����һ������Ϊ��A��
��ͼ����ƽ��ֱ������ϵ�У���CDE�Ķ���C������ΪC��1��-2������D�ĺ�����Ϊ$\frac{19}{5}$������CDE�Ƶ�C��ת����CBO����D�Ķ�Ӧ��B��x���ϣ�������y=ax2+bx+c�Ե�CΪ���㣬�Ҿ�����B������x�����һ������Ϊ��A����1��ͼ�У���OCE=��BCD��
��2���������ߵĽ���ʽ��
��3�����������Ƿ���ڵ�P��ʹS��PAE=$\frac{1}{2}$S��CDE�������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1��������ת�������á�OCE=��BCD��
��2����CH��OE��H����ͼ��������ת�����ʵ�CO=CE��CB=CD��OB=DE�������õ��������ε����ʵ�OH=HE=1����E������Ϊ��2��0������B��m��0����D��$\frac{19}{5}$��n�������������ľ��빫ʽ��CD2=��1-$\frac{19}{5}$��2+��-2-n��2��CB2=��1-m��2+22��DE2=��2-$\frac{19}{5}$��2+n2�����ԣ�1-$\frac{19}{5}$��2+��-2-n��2=��1-m��2+22����2-$\frac{19}{5}$��2+n2=m2�������m��n�ķ�����õ�m=3��n=-$\frac{12}{5}$����B��3��0����Ȼ���趥��ʽy=a��x-1��2-2���ٰ�B������������a���ɵõ������߽���ʽ��
��3�������������ߵĶԳ��Եõ�A��-1��0�����ٸ�����ת�����ʵá�CDE�ա�CBO����S��CDE=S��CBO=3����P��t��$\frac{1}{2}$t2-t-$\frac{3}{2}$�������������������ʽ�õ�$\frac{1}{2}$•3•|$\frac{1}{2}$t2-t-$\frac{3}{2}$|=$\frac{1}{2}$•3����$\frac{1}{2}$t2-t-$\frac{3}{2}$=1��$\frac{1}{2}$t2-t-$\frac{3}{2}$=-1��Ȼ��ֱ�����t��һԪ���η������t���Ӷ��ɵõ�����������P�����꣮
��� �⣺��1���ߡ�CDE�Ƶ�C��ת����CBO��
���OCE=��BCD��
�ʴ�ΪBCD��
��2����CH��OE��H����ͼ��
�ߡ�CDE�Ƶ�C��ת����CBO��
��CO=CE��CB=CD��OB=DE��
��OH=HE=1��
��OE=2��
��E��������2��0����
��B��m��0����D��$\frac{19}{5}$��n����
��CD2=��1-$\frac{19}{5}$��2+��-2-n��2��CB2=��1-m��2+22��DE2=��2-$\frac{19}{5}$��2+n2��
�ࣨ1-$\frac{19}{5}$��2+��-2-n��2=��1-m��2+22����2-$\frac{19}{5}$��2+n2=m2��
��m=3��n=-$\frac{12}{5}$��
��B��3��0����
�������߽���ʽΪy=a��x-1��2-2��
��B��3��0�������4a-2=0�����a=$\frac{1}{2}$��
�������߽���ʽΪy=$\frac{1}{2}$��x-1��2-2����y=$\frac{1}{2}$x2-x-$\frac{3}{2}$��
��3�����ڣ�
A���B����ֱ��x=1�Գƣ�
��A��-1��0����
�ߡ�CDE�Ƶ�C��ת����CBO��
���CDE�ա�CBO��
��S��CDE=S��CBO=$\frac{1}{2}$•2•3=3��
��P��t��$\frac{1}{2}$t2-t-$\frac{3}{2}$����
��S��PAE=$\frac{1}{2}$S��CDE��
��$\frac{1}{2}$•3•|$\frac{1}{2}$t2-t-$\frac{3}{2}$|=$\frac{1}{2}$•3��
��$\frac{1}{2}$t2-t-$\frac{3}{2}$=1��$\frac{1}{2}$t2-t-$\frac{3}{2}$=-1��
�ⷽ��$\frac{1}{2}$t2-t-$\frac{3}{2}$=1��t1=1+$\sqrt{6}$��t2=1-$\sqrt{6}$����ʱP������Ϊ��1+$\sqrt{6}$��1����1-$\sqrt{6}$��1����
�ⷽ��$\frac{1}{2}$t2-t-$\frac{3}{2}$=-1��t1=1+$\sqrt{2}$��t2=1-$\sqrt{2}$����ʱP������Ϊ��1+$\sqrt{2}$��-1����1-$\sqrt{2}$��-1����
��������������������P��������1+$\sqrt{6}$��1����1-$\sqrt{6}$��1����1+$\sqrt{2}$��-1����1-$\sqrt{2}$��-1����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ���ת�����ʣ������ô���ϵ��������κ�������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| �� | �� | �� | �� |
��2������$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}��81��\sqrt{3}-\sqrt{2}+1��$��n����ȡ�õ���С��������4��
 ��ͼ�����κ���y=-x2-2x��ͼ����x�ύ�ڵ�A��O��������������һ��P������S��AOP=3�����P�������ǣ�1��-3����-3��-3����
��ͼ�����κ���y=-x2-2x��ͼ����x�ύ�ڵ�A��O��������������һ��P������S��AOP=3�����P�������ǣ�1��-3����-3��-3����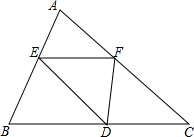 ��ͼ����ABC�У�E��F��D�ֱ���AB��AC��BC�ϵĵ㣬������$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$����S��ABC��S��EFD=25��6��
��ͼ����ABC�У�E��F��D�ֱ���AB��AC��BC�ϵĵ㣬������$\frac{AE}{EB}=\frac{AF}{FC}=\frac{2}{3}$����S��ABC��S��EFD=25��6�� ��ͼ��AC=AD���߶�AB�����߶�CD���е�E����֤��BC=BD��
��ͼ��AC=AD���߶�AB�����߶�CD���е�E����֤��BC=BD��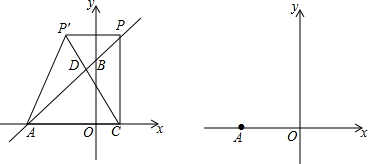
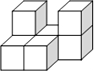 ��ͼ��ʾ�ļ����������߸���ͬ��С��������϶��ɵģ����ĸ���ͼ�ǣ�������
��ͼ��ʾ�ļ����������߸���ͬ��С��������϶��ɵģ����ĸ���ͼ�ǣ�������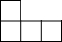



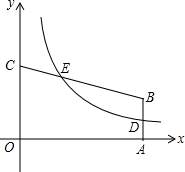 ��ͼ���ı���OABC������ƽ��ֱ������ϵ�У�AB��CO��OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����������y=$\frac{k}{x}��{k��0��x��0}��$��ͼ��AB���е�D��������CB���ڵ�E����֪$\frac{CE}{CB}=\frac{1}{3}��OC=\frac{7}{2}$����AB�ij����ڣ�������
��ͼ���ı���OABC������ƽ��ֱ������ϵ�У�AB��CO��OA����ֱ��Ϊx�ᣬOC����ֱ��Ϊy�ᣬ����������y=$\frac{k}{x}��{k��0��x��0}��$��ͼ��AB���е�D��������CB���ڵ�E����֪$\frac{CE}{CB}=\frac{1}{3}��OC=\frac{7}{2}$����AB�ij����ڣ�������