题目内容
7.已知两个非零的实数m和n,有$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,则$\frac{n}{m}$-$\frac{m}{n}$的值是( )| A. | $\sqrt{21}$ | B. | -$\sqrt{21}$ | C. | $±\sqrt{21}$ | D. | 21 |
分析 先根据题意得出(m+n)2=7mn,故可得出m+n=±$\sqrt{7mn}$,m-n=±$\sqrt{3mn}$,再根据分式混合运算的法则把原式进行化简,再把m+n与m-n代入进行计算即可.
解答 解:∵$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,
∴$\frac{m+n}{mn}$=$\frac{7}{m+n}$,
∴(m+n)2=7mn,(m-n)2=3mn,
∴m+n=±$\sqrt{7mn}$,m-n=±$\sqrt{3mn}$,
∴原式=$\frac{(n+m)(n-m)}{mn}$,
当m+n=$\sqrt{7mn}$,m-n=$\sqrt{3mn}$或m+n=-$\sqrt{7mn}$,m-n=-$\sqrt{3mn}$时,原式=$\sqrt{21}$;
当m+n=-$\sqrt{7mn}$,m-n=$\sqrt{3mn}$或m+n=$\sqrt{7mn}$,m-n=-$\sqrt{3mn}$时,原式=-$\sqrt{21}$.
综上所述,原式=±$\sqrt{21}$.
故选C.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
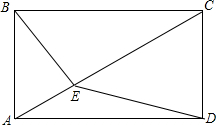 已知E是矩形ABCD对角线AC上一点,且BE=$\sqrt{2}$AE,求证:∠CDE=2∠ABE.
已知E是矩形ABCD对角线AC上一点,且BE=$\sqrt{2}$AE,求证:∠CDE=2∠ABE. 如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.
如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.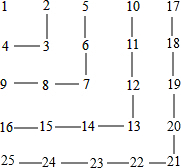 自然数按如表的规律排列:
自然数按如表的规律排列: 如图,△ABC所在的平面上,满足△BCP与△ABC全等的点P共有9个.
如图,△ABC所在的平面上,满足△BCP与△ABC全等的点P共有9个.