题目内容
18.已知x2+5x-7=0,求代数式3x(x-3)-(2x-1)2 的值.分析 原式利用单项式乘以多项式法则,以及完全平方公式化简,去括号合并得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:原式=3x2-9x-4x2+4x-1=-x2-5x-1=-(x2+5x)-1,
由x2+5x-7=0,得到x2+5x=7,
则原式=-7-1=-8.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知a满足|2013-a|+$\sqrt{a-2014}$=a,则a-20132的值是( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
6.若三角形的两边长为2和5,则第三边长m可以是( )
| A. | 3 | B. | 4.1 | C. | 7 | D. | 11 |
10.某商贩购进一批苹果到集贸市场零售,已知卖出的苹果质量m与售价s的关系如下表所示,则s与m之间的关系式为s=0.3m+2,m的取值范围是m≥0.
| 质量m(千克) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 售价s(元) | 2 | 2.3 | 2.6 | 2.9 | 3.2 | 3.5 |
7.已知两个非零的实数m和n,有$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,则$\frac{n}{m}$-$\frac{m}{n}$的值是( )
| A. | $\sqrt{21}$ | B. | -$\sqrt{21}$ | C. | $±\sqrt{21}$ | D. | 21 |
8.为了测试某种型号汽车的性能(车速不超过140km/h),对汽车的“刹车距离”进行测试,测试数据如下表:
(1)观察表格中的数据,估计刹车距离关于刹车时的车速的函数的类型,并确定一个满足这些数据的函数的表达式;
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
| 刹车时的车速x(km/h) | 0 | 10 | 20 | 40 | 60 |
| 刹车距离y(m) | 0 | 0.3 | 1.0 | 3.6 | 7.8 |
(2)若该型号的汽车正在行驶时,发现前方约31m处有一只羊横穿公路,驾驶员紧急刹车,在距羊1m处停下,此时车速为多少?是正常行驶还是超速行驶?
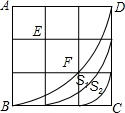 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.