题目内容
15. 如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.
如图,正方形ABCD中,CD=5,BE=CF,且DG2+GE2=28,则AE的长$\sqrt{3}$.
分析 连接DE,由正方形的性质得出AB=BC=CD=DA=5,∠A=∠BCD=∠B=90°,由SAS证明△BCE≌△CDF,得出对应角相等∠BEC=∠CFD,再由角的互余关系证出△DGE是直角三角形,由勾股定理求出DE2,AE2,即可得出AE的长.
解答 解:连接DE,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA=5,∠A=∠BCD=∠B=90°,
在△BCE和△CDF中,
$\left\{\begin{array}{l}{BC=CD}&{\;}\\{∠B=∠FCD}&{\;}\\{BE=CF}&{\;}\end{array}\right.$,
∴△BCE≌△CDF(SAS),
∴∠BEC=∠CFD,
∵∠BEC+∠BCE=90°,
∴∠CFD+∠BCE=90°,
∴∠DGE=∠CGF=90°,
∴DE2=DG2+GE2=28,
∴AE2=DE2-AD2=28-25=3,
∴AE=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若三角形的两边长为2和5,则第三边长m可以是( )
| A. | 3 | B. | 4.1 | C. | 7 | D. | 11 |
10.某商贩购进一批苹果到集贸市场零售,已知卖出的苹果质量m与售价s的关系如下表所示,则s与m之间的关系式为s=0.3m+2,m的取值范围是m≥0.
| 质量m(千克) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 售价s(元) | 2 | 2.3 | 2.6 | 2.9 | 3.2 | 3.5 |
7.已知两个非零的实数m和n,有$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,则$\frac{n}{m}$-$\frac{m}{n}$的值是( )
| A. | $\sqrt{21}$ | B. | -$\sqrt{21}$ | C. | $±\sqrt{21}$ | D. | 21 |
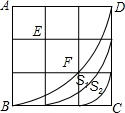 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.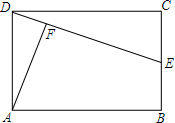 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)