题目内容
12.(1)已知分式$\frac{x-b}{x+a}$,当x=-2时,分式无意义,当x=4时,分式值为0,求a+b的值;(2)当x为何整数时,分式$\frac{6}{x-2}$的值是整数?
分析 (1)根据分母为0是分式无意义,分式值为零的条件是分子等于零且分母不等于零列式计算即可;
(2)写出6的所有公约数,计算即可.
解答 解:(1)要使分式$\frac{x-b}{x+a}$无意义,x+a=0,∵x=-2,∴a=2,
要使分式值为0,则x-b=0,∵x=4,∴b=4,
a+b=6;
(2)要使分式$\frac{6}{x-2}$的值是整数,x-2=-6、-3、-2、-1、1、2、3、6,
则x=-4、-1、0、1、3,4、5、8.
点评 本题考查的是分式为0的条件、分式有意义的条件和求分式的值,掌握分式值为零的条件是分子等于零且分母不等于零是解题的关键,注意列举法求值的应用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2.下列计算正确的是( )
| A. | x2+x=2x2 | B. | (-a2)4=-a12 | C. | (3a3)2=9a6 | D. | x11÷x4•x2=x8 |
7.已知两个非零的实数m和n,有$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,则$\frac{n}{m}$-$\frac{m}{n}$的值是( )
| A. | $\sqrt{21}$ | B. | -$\sqrt{21}$ | C. | $±\sqrt{21}$ | D. | 21 |
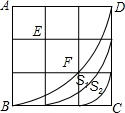 如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.
如图,在3×3方格表中,分别以A、E、F为圆心,半径为3,2,1,圆心角都是90°的三段圆弧与正方形ABCD的边界围成了两个带型,那么这两个带型的面积之比S1:S2=5:3.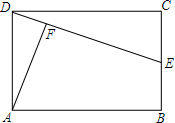 如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1)
如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,证明△AFD∽△DCE,并计算点A至直线DE的距离(精确到0.1) 如图,△ABC≌△BAD,BC=AD.
如图,△ABC≌△BAD,BC=AD.