题目内容
17.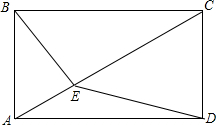 已知E是矩形ABCD对角线AC上一点,且BE=$\sqrt{2}$AE,求证:∠CDE=2∠ABE.
已知E是矩形ABCD对角线AC上一点,且BE=$\sqrt{2}$AE,求证:∠CDE=2∠ABE.
分析 延长BE交CD的延长线于点F,取EF的中点G,连接DG、CG,可得△BAE∽△FCE,根据三角形的相似得出EF和CE的关系,进而证明△ABE∽△GCE,得出∠ABE=∠ECG,证得点A、B、C、G四点共圆,根据点A、B、C、D四点共圆可得A、B、C、D、G五点共圆,得出∠BGD=∠BAD=90°,GD为EF的中垂线,进而证得:∠CDE=2∠ABE.
解答 证明:延长BE交CD的延长线于点F,取EF的中点G,连接DG、CG,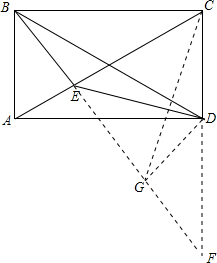
则△BAE∽△FCE,
∴$\frac{EF}{CE}$=$\frac{BE}{AE}$=$\sqrt{2}$,
∴EF=$\sqrt{2}$CE,
∴$\frac{CE}{EG}$=$\frac{CE}{\frac{\sqrt{2}}{2}CE}$=$\sqrt{2}$,
∴$\frac{CE}{EG}$=$\frac{BE}{AE}$,
∴△ABE∽△GCE,
∴∠ABE=∠ECG,
则点A、B、C、G四点共圆,
∵点A、B、C、D四点共圆,
∴点A、B、C、D、G五点共圆,
∴∠BGD=∠BAD=90°,
∴DG垂直平分EF,
∴DE=DF,
∴∠DEF=∠F,
∴∠CDE=∠DEF+∠F=2∠F=2∠ABE.
点评 本题考查了四点共圆的知识:将四点连成一个四边形,若对角互补,那么这四点共圆,解答本题的关键是根据相似三角形的判定和性质得出∠ABE=∠ECG,证得点A、B、C、G四点共圆.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.若不等式mx-2<3x+4的解为x>$\frac{6}{m-3}$,则m的取值范围是( )
| A. | m>3 | B. | m≥3 | C. | m≤3 | D. | m<3 |
8.已知a满足|2013-a|+$\sqrt{a-2014}$=a,则a-20132的值是( )
| A. | 2012 | B. | 2013 | C. | 2014 | D. | 2015 |
2.下列计算正确的是( )
| A. | x2+x=2x2 | B. | (-a2)4=-a12 | C. | (3a3)2=9a6 | D. | x11÷x4•x2=x8 |
6.若三角形的两边长为2和5,则第三边长m可以是( )
| A. | 3 | B. | 4.1 | C. | 7 | D. | 11 |
7.已知两个非零的实数m和n,有$\frac{1}{m}+\frac{1}{n}$=$\frac{7}{m+n}$,则$\frac{n}{m}$-$\frac{m}{n}$的值是( )
| A. | $\sqrt{21}$ | B. | -$\sqrt{21}$ | C. | $±\sqrt{21}$ | D. | 21 |