题目内容
7. 正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )| A. | 2π | B. | 4-2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 0 |
分析 根据图形的运动的轨迹得出:点P的运动路径是两个PP′的长,根据正方形的边长为4,得OB=2,则BP=2$\sqrt{2}$,由图1可知:四边形MBNP′是矩形,则对角线NN=BP′=4,可以求PP′的长.
解答 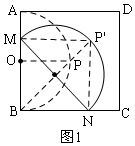 解:在这个运动过程中,点P的运动路径分两个阶段:
解:在这个运动过程中,点P的运动路径分两个阶段:
①点M从A点开始运动到此时的M时,如图1,中点P经过的路线为从P到P′的长,即PP′的长,
∵△BOP′是等腰直角三角形,
∵AB=4,
∴OB=OP=2,
∴BP=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵P为半圆弧的中点,MN为半圆的直径,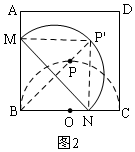
∴MN=BP′=4,
∴PP′=BP′-BP=4-2$\sqrt{2}$;
②当点M继续运动到点B时,如图2,中点P经过的路线为从P′到P的路线长,即也是PP′的长,
综上所述,点P的运动路径长是:2(4-2$\sqrt{2}$)=8-4$\sqrt{2}$;
故选C.
点评 本题考查了正方形的性质、动点的运动轨迹、圆周角定理、等腰直角三角形的性质以及勾股定理,利用数形结合的思想,得出P的运动路线是两个PP′的长是本题的关键.

练习册系列答案
相关题目
17.下列运算中,正确的是( )
| A. | 3x3•2x2=6x6 | B. | (-x2y)2=x4y | C. | (2x2)3=6x6 | D. | x5÷$\frac{1}{2}$x=2x4 |
18. 如图,△AOB缩小后得到△COD,△AOB与△COD的相似比是3,若C(1,2),则点A的坐标为( )
如图,△AOB缩小后得到△COD,△AOB与△COD的相似比是3,若C(1,2),则点A的坐标为( )
 如图,△AOB缩小后得到△COD,△AOB与△COD的相似比是3,若C(1,2),则点A的坐标为( )
如图,△AOB缩小后得到△COD,△AOB与△COD的相似比是3,若C(1,2),则点A的坐标为( )| A. | (2,4) | B. | (2,6) | C. | (3,6) | D. | (3,4) |
2.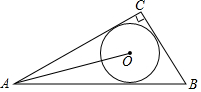 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{\sqrt{2}}{4}$ |
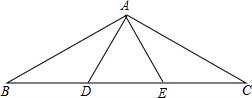 如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是边BC的三等分点,连接AD、AC.则下列结论正确的是①②④.
如图,在△ABC中,AB=AC,∠BAC=120°,点D、E是边BC的三等分点,连接AD、AC.则下列结论正确的是①②④. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.
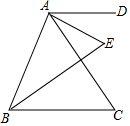 已知,如图,AD∥BC,AE、BE分别平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,则∠E的度数是60°.
已知,如图,AD∥BC,AE、BE分别平分∠DAC和∠ABC.若∠DAC=50°,∠ABC=70°,则∠E的度数是60°.