题目内容
8. 如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.
如图,已知直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,P是以C(0,2)为圆心,2为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是13.
分析 求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.
解答 解:∵直线y=$\frac{3}{4}$x-3与x轴、y轴分别交于A、B两点,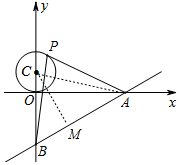
∴A点的坐标为(4,0),B点的坐标为(0,-3),3x-4y-12=0,
即OA=4,OB=3,由勾股定理得:AB=5
过C作CM⊥AB于M,连接AC,
则由三角形面积公式得:$\frac{1}{2}$×AB×CM=$\frac{1}{2}$×OA×OC+$\frac{1}{2}$×OA×OB,
∴5×CM=4×1+3×4,
∴CM=$\frac{16}{5}$,
∴圆C上点到直线y=$\frac{3}{4}$x-3的最大距离是:2+$\frac{16}{5}$=$\frac{26}{5}$,
∴△PAB面积的最大值是$\frac{1}{2}$×5×$\frac{26}{5}$=13,
故答案为:13.
点评 本题考查了三角形的面积,点到直线的距离公式的应用,解此题的关键是求出圆上的点到直线AB的最大距离.

练习册系列答案
相关题目
7. 正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
 正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )| A. | 2π | B. | 4-2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 0 |
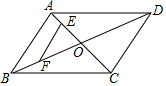 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.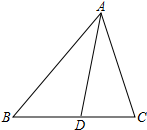 如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.
如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$. 如图,在△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:AD=2:1,DE=6,则AB的长为9.
如图,在△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:AD=2:1,DE=6,则AB的长为9.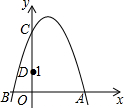 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P在抛物线上,且△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P在抛物线上,且△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).