题目内容
2.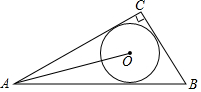 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,⊙O是△ABC的内切圆,连接OA,则sin∠OAB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{\sqrt{2}}{4}$ |
分析 作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,设⊙O的半径为r,先利用勾股定理计算出AB=5,再根据切线的性质得OD=OE=OF=r,易得四边形CEOF为正方形,所以CE=CF=r,则利用切线长定理得到AE=AD=4-r,BF=BD=3-r,所以4-r+3-r=5,解得r=1,于是得到AD=3,然后计算出OA后利用正弦的定义求解.
解答 解:作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,如图,设⊙O的半径为r,
∵∠C=90°,BC=3,AC=4,
∴AB=5,
∵⊙O是△ABC的内切圆,
∴OD=OE=OF=r,
∴四边形CEOF为正方形,
∴CE=CF=r,
∴AE=AD=4-r,BF=BD=3-r,
∴4-r+3-r=5,解得r=1,
∴AD=3,
在Rt△AOD中,OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴sin∠OAD=$\frac{OD}{OA}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$.
故选C.
点评 本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了切线长定理和切线的性质.

练习册系列答案
相关题目
7. 正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
 正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )
正方形ABCD的边长为4,M、N分别是AB、CB上的点,MN=4,以MN为直径做半圆,点P为半圆弧中点,点M从点A开给滑动,到点B停止,在这个运动过程中,点P的运动路径长是( )| A. | 2π | B. | 4-2$\sqrt{2}$ | C. | 8-4$\sqrt{2}$ | D. | 0 |
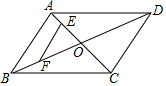 如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.
如图,?ABCD的对角线AC、BD相交于点O,E,F分别是线段AO、BO的中点,若AC+BD=22厘米,△OAB的周长是18厘米,则EF=3.5厘米.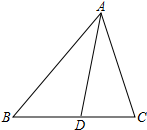 如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$.
如图所示,△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=8,AC=6,则AD的长是$\frac{24\sqrt{3}}{7}$. 如图,在△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:AD=2:1,DE=6,则AB的长为9.
如图,在△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:AD=2:1,DE=6,则AB的长为9. 如图,在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,∠DCB=120°,连接对角线BD,则△ABD的面积为$\frac{\sqrt{11}}{4}$.
如图,在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,∠DCB=120°,连接对角线BD,则△ABD的面积为$\frac{\sqrt{11}}{4}$.