��Ŀ����
��ͼ����A��B��C�����ɡ�ABCƽ�ƺ�õ��ģ���֪��ABC��һ��P(x0��y0)��ƽ�ƺ��Ӧ��P��(x0��5��y0��2)��
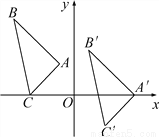
(1)��֪A(��1,2)��B(��4,5)��C(��3,0)����д��A�䡢B�䡢C������ꣻ
(2)��˵����A��B��C��������ɡ�ABCƽ�Ƶõ��ģ�
(3)��ֱ��д����A��B��C������Ϊ6.
 (1)A��Ϊ(4,0)��B��Ϊ(1,3)��C��Ϊ(2����2)��
(2)��ABC������ƽ��5����λ��������ƽ��2����λ(��������ƽ��2����λ��������ƽ��5����λ)��
(3)��A��B��C������Ϊ6.
���������������: ��1�����ݵ�P��x0,y0����ƽ�ƺ��Ӧ��ΪP�䣨x0+5,y0-2���ɵ�A,B,C���������仯����,�����ɵô�,
��2�����ݵ������ı仯���ɿɵá�AB...
(1)A��Ϊ(4,0)��B��Ϊ(1,3)��C��Ϊ(2����2)��
(2)��ABC������ƽ��5����λ��������ƽ��2����λ(��������ƽ��2����λ��������ƽ��5����λ)��
(3)��A��B��C������Ϊ6.
���������������: ��1�����ݵ�P��x0,y0����ƽ�ƺ��Ӧ��ΪP�䣨x0+5,y0-2���ɵ�A,B,C���������仯����,�����ɵô�,
��2�����ݵ������ı仯���ɿɵá�AB...
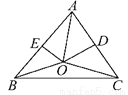
��ͼ�������������ABC�У���BAC��60�㣬��AC��AB�Ĵ�ֱƽ���߽��ڵ�O����AC��AB�ڵ�D��E�����BOC����____.
 120��
����������AB,AC�Ĵ�ֱƽ���߽��ڵ�O,
��OA=OB=OC
���OAB=��OBA,��OAC=��OCA
���OAB+��OAC=��OBA+��OCA=��A=60��
���OBC+��OCB=180��-2*60��=60��
���BOC=180��-60��=120��.
�ʴ��ǣ�120��.
120��
����������AB,AC�Ĵ�ֱƽ���߽��ڵ�O,
��OA=OB=OC
���OAB=��OBA,��OAC=��OCA
���OAB+��OAC=��OBA+��OCA=��A=60��
���OBC+��OCB=180��-2*60��=60��
���BOC=180��-60��=120��.
�ʴ��ǣ�120��. ��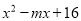 ����ȫƽ��ʽ����ôm=________.
����ȫƽ��ʽ����ôm=________.
 ��8
���������������������x2-mx+16��һ����ȫƽ��ʽ��
��m=��8��
�ʴ�Ϊ����8
��8
���������������������x2-mx+16��һ����ȫƽ��ʽ��
��m=��8��
�ʴ�Ϊ����8 ��ƽ��ֱ������ϵ�У���A�������ǣ�2��3������B�������ǣ�2��-2���������߶�AB����ƽ��3����λ���ΪA��B�䣬��A��B��ɱ�ʾΪ ��
 x=-1��-2��y��3����
��������
����������ߵ�A�������ǣ�2��3������B�������ǣ�2��-2���������߶�AB����ƽ��3����λ���ΪA��B�䣬
���A���������-1��3������B���������-1��-2����
���߶�A��B��ɱ�ʾΪ x=-1��-2��y��3����
x=-1��-2��y��3����
��������
����������ߵ�A�������ǣ�2��3������B�������ǣ�2��-2���������߶�AB����ƽ��3����λ���ΪA��B�䣬
���A���������-1��3������B���������-1��-2����
���߶�A��B��ɱ�ʾΪ x=-1��-2��y��3���� ����ABC�������������ӡ���3�����������������ɵ����������ɡ�ABC��������
A. ����ƽ��3����λ�õ��� B. ����ƽ��3����λ�õ���
C. ����ƽ��3����λ�õ��� D. ����ƽ��3����λ�õ���
 B
����������������
��ABC�������������ӡ���3�������ABC����ƽ��3����λ����ѡB��
B
����������������
��ABC�������������ӡ���3�������ABC����ƽ��3����λ����ѡB�� ����P����ƽ��2����λ��������ƽ��1����λ���õ�P��(��1,3)�����P��������_____.
 (1,2)
���������������������ƽ�����������жϽ����
����P����ƽ��2����λ��������ƽ��1����λ�õ�P��(-1��3)�����P��������(1��2) .
(1,2)
���������������������ƽ�����������жϽ����
����P����ƽ��2����λ��������ƽ��1����λ�õ�P��(-1��3)�����P��������(1��2) . ��֪������y= -x2+mx+��7-2m����mΪ��������
��1��֤��������mΪ��ֵ����������x�����������ͬ�Ľ��㣻
��2������������x��Ľ���A��x1��0����B��x2��0���ľ���ΪAB=4��A��B����ߣ����������߽�y�����������C���������ߵĽ���ʽ��
 ��1��֤������������2�������ߵĽ���ʽΪy= -x2+2x+3��
�������������������1��Ҫ֤����������x�����������ͬ�Ľ���֤�������ߵ��б�ʽ������������֤���б�ʽ���������ɽ�����⣻
��2��������AB=4���Ե�|x2-x1|=4������x2-x1��2=��x2-x1��2-4x1x2=16��Ȼ�����ø���ϵ���Ĺ�ϵ���ɵõ�����m���̣��ⷽ�̼������m��Ҳ������������ߵĽ���ʽ��
����...
��1��֤������������2�������ߵĽ���ʽΪy= -x2+2x+3��
�������������������1��Ҫ֤����������x�����������ͬ�Ľ���֤�������ߵ��б�ʽ������������֤���б�ʽ���������ɽ�����⣻
��2��������AB=4���Ե�|x2-x1|=4������x2-x1��2=��x2-x1��2-4x1x2=16��Ȼ�����ø���ϵ���Ĺ�ϵ���ɵõ�����m���̣��ⷽ�̼������m��Ҳ������������ߵĽ���ʽ��
����... ��֪���κ���y=x2+bx-2��ͼ����x���һ������Ϊ��1��0����������x�����һ�����������ǣ�������
A. ��1��0�� B. ��2��0�� C. ��-2��0�� D. ��-1��0��
 C
�������������������x��1��y��0����y��x2��bx��2�ã�
0��1��b��2��
��b��1��
��Գ���Ϊx������
��x������
��x2����2��
����x�����һ�����������ǣ���2��0����
��ѡC��
C
�������������������x��1��y��0����y��x2��bx��2�ã�
0��1��b��2��
��b��1��
��Գ���Ϊx������
��x������
��x2����2��
����x�����һ�����������ǣ���2��0����
��ѡC�� ������ĸ�У�H��F��A��O��M��W��Y��E����Գ�ͼ�εĸ����ǣ� ��
A. 5 B. 4 C. 6 D. 7
 D
���������ӵ�һ����ĸ�о���ֻҪ�ܹ��ҵ�һ���Գ��ᣬ�������ĸ�������Գ����۵������ߵIJ����ܹ������غϣ�������Գ�ͼ�Σ����Եó�����ĸH��A��O��M��W��Y��E���߸���ĸ��������Գ�ͼ��.
��ѡ��D.
D
���������ӵ�һ����ĸ�о���ֻҪ�ܹ��ҵ�һ���Գ��ᣬ�������ĸ�������Գ����۵������ߵIJ����ܹ������غϣ�������Գ�ͼ�Σ����Եó�����ĸH��A��O��M��W��Y��E���߸���ĸ��������Գ�ͼ��.
��ѡ��D. 
