题目内容
已知二次函数y=x2+bx-2的图象与x轴的一个交点为（1，0），则它与x轴的另一个交点坐标是（ ）
A. （1，0） B. （2，0） C. （-2，0） D. （-1，0）
C
【解析】试题分析：把x＝1，y＝0代入y＝x2＋bx－2得：
0＝1＋b－2，
∴b＝1，
∴对称轴为x＝＝，
∴x＝＝，
∴x2＝－2，
它与x轴的另一个交点坐标是（－2，0）．
故选C．
如果
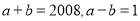，那么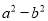
=___________.
2008
【解析】试题解析：∵a2-b2=（a+b）（a-b），
∴把a+b=2008，a-b=1代入上式得：
原式=2008×1=2008．
故答案为：2008． 如图，△A′B′C′是由△ABC平移后得到的，已知△ABC中一点P(x0，y0)经平移后对应点P′(x0＋5，y0－2)．
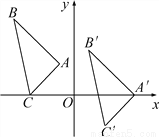
(1)已知A(－1,2)，B(－4,5)，C(－3,0)，请写出A′、B′、C′的坐标；
(2)试说明△A′B′C′是如何由△ABC平移得到的；
(3)请直接写出△A′B′C′的面积为6.
(1)A′为(4,0)、B′为(1,3)、C′为(2，－2)；
(2)△ABC先向右平移5个单位，再向下平移2个单位(或先向下平移2个单位，再向右平移5个单位)；
(3)△A′B′C′的面积为6.
【解析】试题分析: （1）根据点P（x0,y0）经平移后对应点为P′（x0+5,y0-2）可得A,B,C三点的坐标变化规律,进而可得答案,
（2）根据点的坐标的变化规律可得△AB... 如图，抛物线y= -x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y____0（填“＞”“=”或“＜”号）．
＜
【解析】试题分析：根据题意可得函数的对称轴为x=1，∵0＜＜1，则1＜＜2，∴x=－2＜0，根据图象可得：当x＜0时，y＜0. 抛物线y＝－3x2－x＋4与坐标轴的交点个数是( )
A. 3 B. 2 C. 1 D. 0
A
【解析】试题分析：抛物线解析式y=﹣3x2﹣x+4，令x=0，解得：y=4，∴抛物线与y轴的交点为（0，4），
令y=0，得到﹣3x2﹣x+4=0，即3x2+x﹣4=0，分解因式得：（3x+4）（x﹣1）=0，
解得：x1=﹣，x2=1，∴抛物线与x轴的交点分别为（﹣，0），（1，0），
综上，抛物线与坐标轴的交点个数为3．故选：A． 二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A. 1 B. -1 C. -2 D. 0
B
【解析】试题分析：先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0，求出k的值，再根据根与系数的关系即可求出另一个解x2的值．
【解析】
∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得，
﹣9+6+k=0，解得k=3，
∴原方程可化为：﹣x2+2x+3=0，
∴x1+x2=3+x2=﹣=2，解得x2=﹣1．
故选B． 若|a﹣2|+b2﹣2b+1=0，则a=__，b=__．
2 1
【解析】∵|a﹣2|+b2﹣2b+1=0，
∴|a﹣2|+(b-1)2=0，
∴a-2=0,b-1=0,
∴a=2,b=1. 已知M、N是线段AB的垂直平分线上任意两点，则∠MAN和∠MBN之间关系是____.
∠MAN=∠MBN
【解析】∵原题当中没有说明点M、N在线段AB的位置，
∴可能有以下四种情况：
①如图①，点M、N在线段AB两侧时，
∵M、N是线段AB的垂直平分线上任意两点，
∴点A、B两点关于直线MN轴对称，
∴线段MA、MB两点关于直线MN轴对称，
同理线段NA、NB两点关于直线MN轴对称，
∴△MAN与△MBN关于直线MN轴对称，
∴... 如图，在活动课上，小明和小红合作用一副三角板来测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，他调整自己的位置，设法使得三角板的一条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．求出旗杆MN的高度．（参考数据：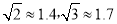 
，结果保留整数．）
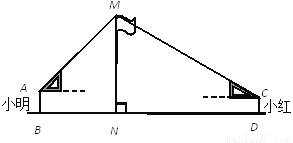
旗杆高约为12米．
【解析】试题分析：过点A作AE⊥MN于E，过点C作CF⊥MN于F，则EF=0.2m．由△AEM是等腰直角三角形得出AE=ME，设AE=ME=xm，则MF=(x+0.2)m，FC=(28-x)m．在Rt△MFC中，由MF=CF•tan∠MCF，解方程求出x的值，则MN=ME+EN．
试题解析： 过点A作AE⊥MN于E，
过点C作CF⊥MN于F
则EF= =...