题目内容
若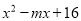 是完全平方式,那么m=________.
是完全平方式,那么m=________.
 ±8
【解析】试题解析:∵若x2-mx+16是一个完全平方式,
∴m=±8,
故答案为:±8
±8
【解析】试题解析:∵若x2-mx+16是一个完全平方式,
∴m=±8,
故答案为:±8
练习册系列答案
相关题目
口袋中有9个球,其中4个红球,3个蓝球,2个白球,在下列事件中,发生的可能性为1的是( )
A. 从口袋中拿一个球恰为红球 B. 从口袋中拿出2个球都是白球
C. 拿出6个球中至少有一个球是红球 D. 从口袋中拿出的5个球恰为3红2白
 C
【解析】对于A,从口袋中拿一个球恰为红球,可能性小于1,故不符合题意;
对于B,从口袋中拿出2个球都是白球,这是一个随机事件,发生的可能性小于1,故不符合题意;
对于C,拿出6个球中,至少有一个球是红球是正确的,因为蓝球3个,白球5个,如果在极端情况下,这6个球尽可能的不是红球,那么最多有五个不是红球,至少有一个是红球,所以C正确.
对于D, 从口袋中拿出的5个球恰为3...
C
【解析】对于A,从口袋中拿一个球恰为红球,可能性小于1,故不符合题意;
对于B,从口袋中拿出2个球都是白球,这是一个随机事件,发生的可能性小于1,故不符合题意;
对于C,拿出6个球中,至少有一个球是红球是正确的,因为蓝球3个,白球5个,如果在极端情况下,这6个球尽可能的不是红球,那么最多有五个不是红球,至少有一个是红球,所以C正确.
对于D, 从口袋中拿出的5个球恰为3... 判断对错:轴对称图形也是中心对称图形;__________________
 错
【解析】有的图形是轴对称图形但不一定是中心对称图形,例如等腰三角形.
故答案:错.
错
【解析】有的图形是轴对称图形但不一定是中心对称图形,例如等腰三角形.
故答案:错. 如果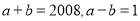 ,那么
,那么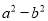 =___________.
=___________.
 2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008.
2008
【解析】试题解析:∵a2-b2=(a+b)(a-b),
∴把a+b=2008,a-b=1代入上式得:
原式=2008×1=2008.
故答案为:2008. 若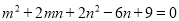 ,则
,则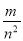 的值为______________
的值为______________
 【解析】∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0,
∴m+n=0且n-3=0,
∴m=-3,n=3,
∴,
故答案为-.
【解析】∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0,
∴m+n=0且n-3=0,
∴m=-3,n=3,
∴,
故答案为-. 若a、b、c是△ABC的三边,满足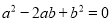 且
且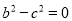 ,则△ABC的形状是( )
,则△ABC的形状是( )
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等边三角形
 D
【解析】∵a2-2ab+b2=0且b2-c2=0,∴(a-b)2=0且(b+c)(b-c)=0,
∴a=b且b=c,即a=b=c,∴△ABC为等边三角形,
故选D.
D
【解析】∵a2-2ab+b2=0且b2-c2=0,∴(a-b)2=0且(b+c)(b-c)=0,
∴a=b且b=c,即a=b=c,∴△ABC为等边三角形,
故选D. 下列各式中不能用平方差公式分解的是( )
A. 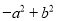 B.
B. 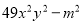 C.
C. 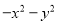 D.
D. 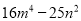
 C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C.
C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C. 如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
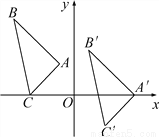
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
 (1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB...
(1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB... 若|a﹣2|+b2﹣2b+1=0,则a=__,b=__.
 2 1
【解析】∵|a﹣2|+b2﹣2b+1=0,
∴|a﹣2|+(b-1)2=0,
∴a-2=0,b-1=0,
∴a=2,b=1.
2 1
【解析】∵|a﹣2|+b2﹣2b+1=0,
∴|a﹣2|+(b-1)2=0,
∴a-2=0,b-1=0,
∴a=2,b=1. 
