题目内容
将△ABC各顶点的纵坐标加“﹣3”,连接这三点所成的三角形是由△ABC( )
A. 向上平移3个单位得到的 B. 向下平移3个单位得到的
C. 向左平移3个单位得到的 D. 向右平移3个单位得到的
 B
【解析】【解析】
△ABC各顶点的纵坐标加“﹣3”,则△ABC向下平移3个单位。故选B.
B
【解析】【解析】
△ABC各顶点的纵坐标加“﹣3”,则△ABC向下平移3个单位。故选B.
如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交AB于点E,交BC于点F.若BF=3cm.求BC.
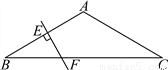
 9cm
【解析】试题分析:先根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°,根据线段垂直平分线性质和等腰三角形性质求出∠BAF=30°,根据含30度角的直角三角形性质求出AF、FC即可.
试题解析:
∵在△ABC中,AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵AB的垂直平分线EF,
∴AF=BF,
∴∠BAF=∠B=30°,
又∵BF=3...
9cm
【解析】试题分析:先根据等腰三角形性质和三角形内角和定理求出∠B=∠C=30°,根据线段垂直平分线性质和等腰三角形性质求出∠BAF=30°,根据含30度角的直角三角形性质求出AF、FC即可.
试题解析:
∵在△ABC中,AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵AB的垂直平分线EF,
∴AF=BF,
∴∠BAF=∠B=30°,
又∵BF=3... 若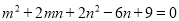 ,则
,则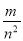 的值为______________
的值为______________
 【解析】∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0,
∴m+n=0且n-3=0,
∴m=-3,n=3,
∴,
故答案为-.
【解析】∵m2+2mn+2n2-6n+9=0
∴(m+n)2+(n-3)2=0,
∴m+n=0且n-3=0,
∴m=-3,n=3,
∴,
故答案为-. 下列各式中不能用平方差公式分解的是( )
A. 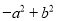 B.
B. 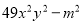 C.
C. 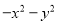 D.
D. 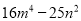
 C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C.
C
【解析】A选项-a2+b2=b2-a2=(b+a)(b-a);B选项49x2y2-m2=(7xy+m)(7xy-m);C选项-x2-y2是两数的平方和,不能进行分解因式;D选项16m4-25n2=(4m)2-(5n)2=(4m+5n)(4m-5n),
故选C. 如图的平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(4,3),B(3,1),C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,分别得到A1、B1、C1,依次连接A1,B1,C1,各点,请写出A1、B1、C1的坐标并画出△A1B1C1,并判断所得三角形A1B1C1与三角形ABC的大小、形状和位置有什么关系?
(2)将三角形ABC三个顶点的纵坐标都减去5,分别得到A2、B2、C2,依次连接A2,B2,C2,各点,请写出A2、B2、C2的坐标并画出△A2B2C2,并判断所得三角形A2B2C2与三角形ABC的大小、形状和位置有什么关系?
(3)求△A2B2C2的面积.
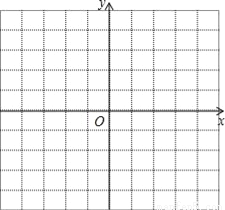
 (1)(2)见解析;(3)
【解析】试题分析:(1)在坐标系内画出△ABC与△A1B1C1,再写出A1、B1、C1的坐标即可;
(2)画出△A2B2C2,再写出A2、B2、C2的坐标即可;
(3)根据三角形的面积公式得出△A2B2C2的面积即可.
试题解析:【解析】
(1)如图所示:
A1(﹣2,3),B1(﹣3,1),C1(﹣5,2),
所得三角形与原三角形...
(1)(2)见解析;(3)
【解析】试题分析:(1)在坐标系内画出△ABC与△A1B1C1,再写出A1、B1、C1的坐标即可;
(2)画出△A2B2C2,再写出A2、B2、C2的坐标即可;
(3)根据三角形的面积公式得出△A2B2C2的面积即可.
试题解析:【解析】
(1)如图所示:
A1(﹣2,3),B1(﹣3,1),C1(﹣5,2),
所得三角形与原三角形... 如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点P′(x0+5,y0-2).
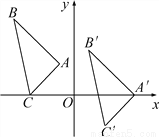
(1)已知A(-1,2),B(-4,5),C(-3,0),请写出A′、B′、C′的坐标;
(2)试说明△A′B′C′是如何由△ABC平移得到的;
(3)请直接写出△A′B′C′的面积为6.
 (1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB...
(1)A′为(4,0)、B′为(1,3)、C′为(2,-2);
(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);
(3)△A′B′C′的面积为6.
【解析】试题分析: (1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0-2)可得A,B,C三点的坐标变化规律,进而可得答案,
(2)根据点的坐标的变化规律可得△AB... 将点A(1,-3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为____.
 (-2,2).
【解析】∵点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到点A′,∴点A′的横坐标为1﹣3=﹣2,纵坐标为﹣3+5=2,∴A′的坐标为(﹣2,2).故答案为:(﹣2,2).
(-2,2).
【解析】∵点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到点A′,∴点A′的横坐标为1﹣3=﹣2,纵坐标为﹣3+5=2,∴A′的坐标为(﹣2,2).故答案为:(﹣2,2). 抛物线y=-3x2-x+4与坐标轴的交点个数是( )
A. 3 B. 2 C. 1 D. 0
 A
【解析】试题分析:抛物线解析式y=﹣3x2﹣x+4,令x=0,解得:y=4,∴抛物线与y轴的交点为(0,4),
令y=0,得到﹣3x2﹣x+4=0,即3x2+x﹣4=0,分解因式得:(3x+4)(x﹣1)=0,
解得:x1=﹣,x2=1,∴抛物线与x轴的交点分别为(﹣,0),(1,0),
综上,抛物线与坐标轴的交点个数为3.故选:A.
A
【解析】试题分析:抛物线解析式y=﹣3x2﹣x+4,令x=0,解得:y=4,∴抛物线与y轴的交点为(0,4),
令y=0,得到﹣3x2﹣x+4=0,即3x2+x﹣4=0,分解因式得:(3x+4)(x﹣1)=0,
解得:x1=﹣,x2=1,∴抛物线与x轴的交点分别为(﹣,0),(1,0),
综上,抛物线与坐标轴的交点个数为3.故选:A. 一个等腰三角形的顶角为钝角,则底角a的范围是( )
A. 0°<a<9 B. 30°<a<90° C. 0°<a<45° D. 45°<a<90°
 C
【解析】:∵等腰三角形顶角为钝角
∴顶角大于90°小于180°
∴两个底角之和大于0°小于90°
∴每个底角大于0°小于45°
故选:C
C
【解析】:∵等腰三角形顶角为钝角
∴顶角大于90°小于180°
∴两个底角之和大于0°小于90°
∴每个底角大于0°小于45°
故选:C 
