题目内容
将点P向左平移2个单位，再向上平移1个单位，得到P′(－1,3)，则点P的坐标是_____.
(1,2)
【解析】试题分析：根据平移特征即可判断结果。
将点P向左平移2个单位，再向上平移1个单位得到P′(-1，3)，则点P的坐标是(1，2) .
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
26个大写英文字母中有多少个是中心对称图形？
7个
【解析】【试题分析】根据中心对称图形的定义可知：把图形度旋转180度，旋转后的图形能喝原来的图形重合进行判断.
【试题解析】分别是H、I、N、O、S、X、Z； 若a、b、c是△ABC的三边，满足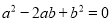
且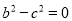
，则△ABC的形状是（ ）
A. 直角三角形 B. 等腰三角形 C. 等腰直角三角形 D. 等边三角形
D
【解析】∵a2-2ab+b2=0且b2-c2=0，∴（a-b）2=0且（b+c）（b-c）=0，
∴a=b且b=c，即a=b=c，∴△ABC为等边三角形，
故选D． 在平面直角坐标系中，将图形沿x轴正方向平移3个单位，变化前后对应点 纵坐标不变， 横坐标增加3个单位．
纵；横
【解析】
试题分析：图形沿x轴正方向平移，改变的是y值，x值不变。 如图，△A′B′C′是由△ABC平移后得到的，已知△ABC中一点P(x0，y0)经平移后对应点P′(x0＋5，y0－2)．
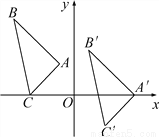
(1)已知A(－1,2)，B(－4,5)，C(－3,0)，请写出A′、B′、C′的坐标；
(2)试说明△A′B′C′是如何由△ABC平移得到的；
(3)请直接写出△A′B′C′的面积为6.
(1)A′为(4,0)、B′为(1,3)、C′为(2，－2)；
(2)△ABC先向右平移5个单位，再向下平移2个单位(或先向下平移2个单位，再向右平移5个单位)；
(3)△A′B′C′的面积为6.
【解析】试题分析: （1）根据点P（x0,y0）经平移后对应点为P′（x0+5,y0-2）可得A,B,C三点的坐标变化规律,进而可得答案,
（2）根据点的坐标的变化规律可得△AB... 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
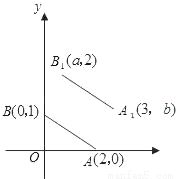
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A. 如图，抛物线y= -x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y____0（填“＞”“=”或“＜”号）．
＜
【解析】试题分析：根据题意可得函数的对称轴为x=1，∵0＜＜1，则1＜＜2，∴x=－2＜0，根据图象可得：当x＜0时，y＜0. 二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A. 1 B. -1 C. -2 D. 0
B
【解析】试题分析：先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0，求出k的值，再根据根与系数的关系即可求出另一个解x2的值．
【解析】
∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得，
﹣9+6+k=0，解得k=3，
∴原方程可化为：﹣x2+2x+3=0，
∴x1+x2=3+x2=﹣=2，解得x2=﹣1．
故选B． 下列4个图形中，不是轴对称图形的是（ ）
A. 有2个内角相等的三角形 B. 有1个内角为30°的直角三角形
C. 有2个内角分别为30°和120°的三角形 D. 线段
B
【解析】A.有2个内角相等的三角形，是等腰三角形，是轴对称图形，不符合题意；
B.有1个内角为30°的直角三角形，三个角度数分别为30°、90°、60°，不是等腰三角形，故不是轴对称图形，符合题意；
C.有2个内角分别为30°和120°的三角形，三个角度数分别为30°、120°、30°，是等腰三角形，是轴对称图形，不符合题意；
D.线段是以其垂直平分线为对称轴，另一条对...