题目内容
12.若一组数据的平均数为3,方差为2,则x12+x22+x32+x42+x52=55.分析 首先根据这组数据的平均数为3,求出x1+x2+x3+x4+x5的和是多少;然后根据方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],适当变形,求出x12+x22+x32+x42+x52的值是多少即可.
解答 解:∵这组数据的平均数为3,
∴x1+x2+x3+x4+x5=3×5=15;
∵这组数据的方差为2,
∴S2=$\frac{1}{5}$[(x1-3)2+(x2-3)2+…+(x5-3)2]
=$\frac{1}{5}$[x12+x22+x32+x42+x52-6(x1+x2+x3+x4+x5)+9×5]
=$\frac{1}{5}$[x12+x22+x32+x42+x52-6×15+45]
=$\frac{1}{5}$[x12+x22+x32+x42+x52-45]
=2
∴x12+x22+x32+x42+x52
=2×5+45
=10+45
=55
故答案为:55.
点评 此题主要考查了平均数的含义和求法,以及方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],要熟练掌握.

练习册系列答案
相关题目
2.下列关系中的两个量成正比例的是( )
| A. | 百米赛跑中的速度与时间 | |
| B. | 圆的面积与半径 | |
| C. | 买同样的水果所要的钱数与水果的质量 | |
| D. | 等腰三角形的周长于腰长 |
3.下列数据是按一定规律排列的:
第一行:1
第二行:2 3
第三行:4 5 6
第四行:7 8 9 10
…
若正整数2016位于第a行,从左数第b个数,则a+b的值为( )
第一行:1
第二行:2 3
第三行:4 5 6
第四行:7 8 9 10
…
若正整数2016位于第a行,从左数第b个数,则a+b的值为( )
| A. | 53 | B. | 126 | C. | 2015 | D. | 1892 |
20.已知数据8,10,x,10的中位数和平均数相等,那么这组数据的中位数是( )
| A. | 9 | B. | 8 | C. | 10 | D. | 8或12 |
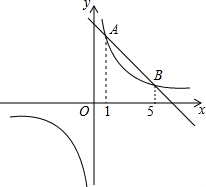 如图,直线y1=k1x-b,与双曲线y2=$\frac{{k}^{2}}{x}$交于A,B两点,它们的横坐标分别为1和5,则不等式k1x>$\frac{{k}^{2}}{x}$+b的解集为x<0或1<x<5.
如图,直线y1=k1x-b,与双曲线y2=$\frac{{k}^{2}}{x}$交于A,B两点,它们的横坐标分别为1和5,则不等式k1x>$\frac{{k}^{2}}{x}$+b的解集为x<0或1<x<5.
 发现问题:
发现问题: