题目内容
1.如图1,矩形ABCD的对角线AC、BD相交于点O,若把矩形ABCD用橡皮擦去一部分,变成图2,从中你发现什么现象?(1)请用语言表达你发现的规律;
(2)简单说明你发现的规律的正确性.
(3)利用(1)的结论,说明图③所示的△ABC中,若BD⊥AC于D,CE⊥AB于E,M为BC的中点,则有MD=ME.
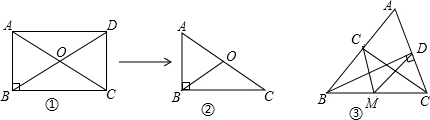
分析 (1)语言描述:直角三角形斜边上的中线等于斜边的一半;
(2)根据矩形的性质可知矩形对角线相等且互相平分,又知矩形一角为90°,故可知直角三角形斜边上的中线等于斜边的一半;
(3)根据(1)中的结论得出EM=$\frac{1}{2}$BC,DM=$\frac{1}{2}$BC,进而得出MD=ME.
解答 解:(1)语言描述:直角三角形斜边上的中线等于斜边的一半.
(2)∵矩形对角线相等且互相平分,
∴AC=BD,BO=DO=$\frac{1}{2}$BD,
∴BO=$\frac{1}{2}$AC,
又∵BO是RT△ABC斜边AC边上的中线,
∴直角三角形斜边上的中线等于斜边的一半.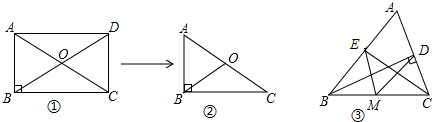
(3)∵△ABC中,BD⊥AC于D,CE⊥AB于E,
∴△BCD和△BCE均为直角三角形,
又∵M为BC的中点,
∴EM=$\frac{1}{2}$BC,DM=$\frac{1}{2}$BC,
∴MD=ME.
点评 本题主要考查了矩形的性质的运用,解答本题的关键是熟练掌握矩形的对角线性质:矩形的对角线相等.由矩形的性质,可以得到直角三角线的一个重要性质,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目
16.2015年12月25日,由叙永县委宣传部、叙永县教育局联合举办的“叙永县第二十一届中学生读好书故事演讲比赛”在县青少年宫举行.李老师为了解该县某校学生每周阅读课外书籍的时间,随机抽取并统计了该校40名学生的阅读情况,如表所示,则阅读时间不少于4h的人数占统计人数的( )
| 阅读时间t/h | 0≤t<2 | 2≤t<4 | 4≤t<6 | 6≤t<8 |
| 频数 | 5 | 11 | 4 |
| A. | 12.5% | B. | 40% | C. | 50% | D. | 60% |
6.某小组7位学生的中考体育测试成绩(满分60分)依次为57,60,59,57,60,58,60,则这组数据的众数与中位数分别是( )
| A. | 60,59 | B. | 60,57 | C. | 59,60 | D. | 60,58 |
13.下列调查中,需用全面调查的是( )
| A. | 调查某市中学生立定跳远的情况 | |
| B. | 调查某市市民对央视春晚的喜爱程度 | |
| C. | 调查某市市民的晨练情况 | |
| D. | 调查某班学生校服的尺寸 |
