题目内容
2. 发现问题:
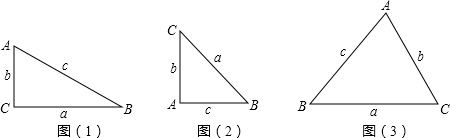
发现问题:如图(1),在△ABC中,∠A=2∠B,且∠A=60°.
我们可以进行以下计算:
由题意可知:∠B=30°,∠C=90°,
可得到:c=2b,a=$\sqrt{3}$b,
所以a2-b2=($\sqrt{3}$b)2-b2=2b2=b•c.
即a2-b2=bc.
提出猜想:
(1)(验证特殊三角形)如图(2),请你参照上述研究方法,对等腰直角三角形进行验证,判断猜想是否正确,并写出验证过程;
已知:△ABC中,∠A=2∠B,∠A=90°
求证:a2-b2=bc.
(2)(验证一般三角形)如图(3),
已知:△ABC中,∠A=2∠B,
求证:a2-b2=bc.
结论应用:
若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
分析 (1)由等腰直角三角形的性质得出b=c,∠A=90°,由勾股定理得出a2=2b2,即可得出结论;
(2)作,∠A的平分线AD,则∠1=∠2=$\frac{1}{2}$∠A,由已知条件得出∠B=∠1=∠2,得出BD=AD,证明△ABC∽△DAC,得出对应边成比例,得出BD=AD=$\frac{bc}{a}$,b2=a•CD,即可得出结论;
(3)设三角形的三边长为2n-2,2n,2n+2,由(2)得出(2n+2)2-(2n-2)2=2n(2n-2),解方程求出n的值,即可得出结果.
解答 (1)证明:∵△ABC是等腰直角三角形,
∴b=c,∠A=90°,
∴a2=b2+c2=2b2,
∴a2-b2=2b2-b2═b2=bc;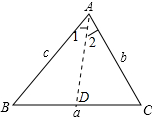 (2)证明:作,∠A的平分线AD,如图所示:
(2)证明:作,∠A的平分线AD,如图所示:
则∠1=∠2=$\frac{1}{2}$∠A,
∵∠A=2∠B,
∴∠B=∠1=∠2,
∴BD=AD,
∵∠C=∠C,
∴△ABC∽△DAC,
∴$\frac{c}{AD}=\frac{b}{CD}=\frac{a}{b}$,
∴BD=AD=$\frac{bc}{a}$,b2=a•CD,
∴a2-b2=a2-a•CD=a(a-CD)=a•BD=a′$\frac{bc}{a}$=bc;
(3)解:a=12,b=8,c=10;理由如下:
设三角形的三边长为2n-2,2n,2n+2,
∵∠A=2∠B,
∴由(2)得:(2n+2)2-(2n-2)2=2n(2n-2),
解得:n=5,或n=0(舍去),
∴n=5,2n-2=8,2n=10,2n+2=12,
∴a=12,b=8,c=10.
点评 本题考查了等腰直角三角形的性质、相似三角形的判定与性质、等腰三角形的判定、勾股定理等知识;熟练掌握相似三角形的性质是解决问题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
13.下列调查中,需用全面调查的是( )
| A. | 调查某市中学生立定跳远的情况 | |
| B. | 调查某市市民对央视春晚的喜爱程度 | |
| C. | 调查某市市民的晨练情况 | |
| D. | 调查某班学生校服的尺寸 |
14.数据:2,5,4,5,3,5,4的众数与中位数分别是( )
| A. | 4,3 | B. | 4,5 | C. | 3,4 | D. | 5,4 |

 在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“变换点”P′的坐标.定义如下:当a≥b时,P’点坐标为(b,-a);当a<b时,P′点坐标为(a,-b).
在平面直角坐标系xOy中,点P的坐标为(a,b),点P的“变换点”P′的坐标.定义如下:当a≥b时,P’点坐标为(b,-a);当a<b时,P′点坐标为(a,-b).