题目内容
在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.已知AE=5,tan∠AED=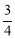 ,则BE+CE= .
,则BE+CE= .
 6或16
【解析】
试题分析:有两种情形,需要分类讨论:
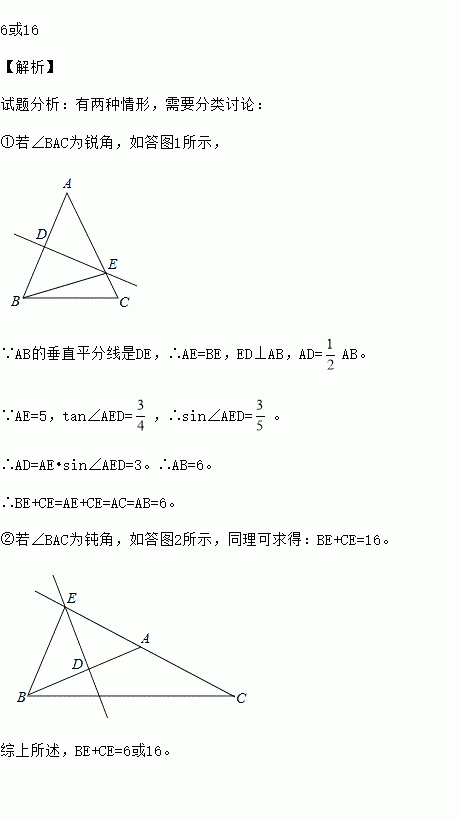
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B...
6或16
【解析】
试题分析:有两种情形,需要分类讨论:
①若∠BAC为锐角,如答图1所示,
∵AB的垂直平分线是DE,∴AE=BE,ED⊥AB,AD=AB。
∵AE=5,tan∠AED=,∴sin∠AED=。
∴AD=AE•sin∠AED=3。∴AB=6。
∴BE+CE=AE+CE=AC=AB=6。
②若∠BAC为钝角,如答图2所示,同理可求得:B...
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列事件中,属于必然事件的是( )
A.随意抛掷一枚骰子,掷得偶数点
B.从一副扑克牌抽出一张,抽得红桃牌
C.任意选择电视的某一频道,正在播放动画片
D.在同一年出生的367名学生中,至少有两个人同月同日生
 D
【解析】
试题解析:A、随意抛掷一枚骰子,掷得偶数点是随机事件,故A错误;
B、从一副扑克牌抽出一张,抽得红桃牌是随机事件,故B错误;
C、任意选择电视的某一频道,正在播放动画片是随机事件,故C错误;
D、在同一年出生的367名学生中,至少有两个人同月同日生是必然事件,故D正确;
故选D.
D
【解析】
试题解析:A、随意抛掷一枚骰子,掷得偶数点是随机事件,故A错误;
B、从一副扑克牌抽出一张,抽得红桃牌是随机事件,故B错误;
C、任意选择电视的某一频道,正在播放动画片是随机事件,故C错误;
D、在同一年出生的367名学生中,至少有两个人同月同日生是必然事件,故D正确;
故选D. 如图,在△ABC中,∠C=90°,D为BC上一点,且DE⊥AB于E,AC=AE.求证:AD平分∠BAC.
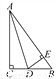
 见解析
【解析】试题分析:证明Rt△ACD≌Rt△AED,利用全等三角形的性质即可得.
试题解析:∵DE⊥AB,∴∠AED=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠CAD=∠EAD,
即AD平分∠BAC.
见解析
【解析】试题分析:证明Rt△ACD≌Rt△AED,利用全等三角形的性质即可得.
试题解析:∵DE⊥AB,∴∠AED=90°,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴∠CAD=∠EAD,
即AD平分∠BAC. 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上,那么sinα=_.
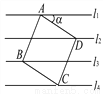
 【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵...
【解析】过D作EF⊥l1,交l1于E,交l4于F,
∵EF⊥l1,l1∥l2∥l3∥l4,
∴EF和l2,l3,l4的夹角都是90°,
即EF与l2,l3,l4都垂直,
∴DE=1,DF=2.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=CD,
∴∠ADE+∠CDF=90°,
又∵∠α+∠ADE=90°,
∴∠α=∠CDF,
∵... 如图,直线y=2x+2与y轴交于A点,与反比例函数y=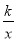 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
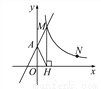
(1)求k的值;
(2)点N(a,1)是反比例函数y=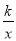 (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
 (1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(1)4;(2)P(,0)
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
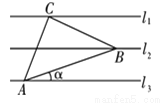
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置. 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sina的值是( )
A. 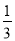 B.
B. 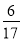 C.
C. 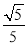 D.
D. 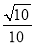
 D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。
D
【解析】如图,分别过点A,B作AE⊥l1,BF⊥l1,垂足分别为E,F,BF与l3交于点D,
则易由AAS证明△AEC≌△CFB。
设平行线间距离为d=1,
则CE=BF=1,AE=CF=2,AC=BC=,AB=。
∴。故选D。 已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°,求证:DA⊥AB.
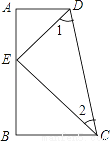
 证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD...
证明见解析.
【解析】试题分析:根据CE平分∠BCD,DE平分∠CDA,得出∠1+∠2=(∠ADC+∠BCD)=90°,∠ADC+∠BCD=180°,证出AD∥BC,再根据CB⊥AB,即可得出DA⊥AB.
【解析】
∵CE平分∠BCD,DE平分∠CDA,
∴∠1=∠ADC,∠2=∠BCD,
∴∠1+∠2=∠ADC+∠BCD=(∠ADC+∠BCD)=90°,
∴∠AD... 如图,AB∥CD,AD∥BC,则图中与∠A相等的角有_____个.
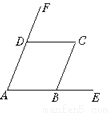
 3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个.
3
【解析】∵AB∥CD,
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC,
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个. 在下列计算中,不能用平方差公式计算的是( )
A. (m-n)(-m+n) B. 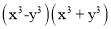
C. (-a-b)(a-b) D. 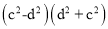
 A
【解析】运用平方差公式计算的两个多项式必须满足一项是相同,另一项互为相反数.选项B、C、D都符合要求,能用平方差公式计算;选项A中m和-m符号相反,n和-n符号相反,不符合要求,不能用平方差公式计算,故选A.
A
【解析】运用平方差公式计算的两个多项式必须满足一项是相同,另一项互为相反数.选项B、C、D都符合要求,能用平方差公式计算;选项A中m和-m符号相反,n和-n符号相反,不符合要求,不能用平方差公式计算,故选A.