题目内容
如图,MP,NQ分别垂直平分AB,AC,且BC=6 cm,则△APQ的周长为( )
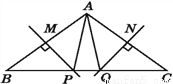
A. 12 cm B. 6 cm C. 8 cm D. 无法确定
B
【解析】由MP、NQ分别垂直平分AB、AC，根据线段垂直平分线的性质，可得BP=AP，CQ=AQ，继而求得△APQ的周长等于BC．
【解析】
∵MP、NQ分别垂直平分AB、AC，
∴BP=AP，CQ=AQ，
∵BC=6cm，
∴△APQ的周长为：AP+PQ+AQ=BP+PQ+CQ=BC=6cm.
故选B.
练习册系列答案
相关题目
你能将下图分成形状相同、大小相同的12块吗？
不要满足于一种分法哦，把你的方法和其它同学交流一下，一定会有更多的收获.
见解析
【解析】试题分析：把所给图形看作是3个正方形，要分成形状、大小相同的12块，需要把每个正方形分成形状、大小相同的4块即可．
试题解析：∵要求分成全等的12块，，
∴每个小正方形要分成全等的四块. 下列事件中，属于必然事件的是（ ）
A．随意抛掷一枚骰子，掷得偶数点
B．从一副扑克牌抽出一张，抽得红桃牌
C．任意选择电视的某一频道，正在播放动画片
D．在同一年出生的367名学生中，至少有两个人同月同日生
D
【解析】
试题解析：A、随意抛掷一枚骰子，掷得偶数点是随机事件，故A错误；
B、从一副扑克牌抽出一张，抽得红桃牌是随机事件，故B错误；
C、任意选择电视的某一频道，正在播放动画片是随机事件，故C错误；
D、在同一年出生的367名学生中，至少有两个人同月同日生是必然事件，故D正确；
故选D． 如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）
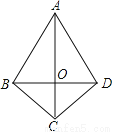
A. 1对 B. 2对 C. 3对 D. 4对
C
【解析】试题分析：在△ABC和△ADC中，根据全等三角形的判定SSS可得△ABC≌△ADC（SSS），根据全等三角形的性质可得∠BAC=∠DAC，∠BCA=∠DCA，在△ABO和△ADO中，可得△ABO≌△ADO（SAS），然后在△BOC和△DOC中，可得△BOC≌△DOC（SAS），
故选：C． 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
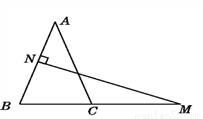
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
(1) 20°；(2) 35°；
(3)规律:∠NMB=∠A.
【解析】（1）根据等边对等角，由AB=AC可得到∠ABM=∠ACB，再结合已知∠A的度数，即可求出∠NMB的度数；
（2）仿照第（1）问的求解过程即可得到∠NMB的度数；
（3）结合上述两问的解答，即可发现∠NMB和∠A之间的大小关系，然后仿照上述解答过程进行验证即可.
【解析】
（1）∵AB=AC，
... 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为（ ）
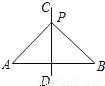
A. 6 B. 5 C. 4 D. 3
B
【解析】因为线段垂直平分线上的点与这条线段两个端点的距离相等，所以PA=PB，则PB=5.
故选B. 如图，在△ABC中，∠C＝90°，D为BC上一点，且DE⊥AB于E，AC＝AE.求证：AD平分∠BAC.
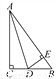
见解析
【解析】试题分析：证明Rt△ACD≌Rt△AED，利用全等三角形的性质即可得.
试题解析：∵DE⊥AB，∴∠AED=90°，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠CAD=∠EAD，
即AD平分∠BAC. 如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1.如果正方形ABCD的四个顶点分别在四条直线上，那么sinα＝＿．
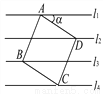
【解析】过D作EF⊥l1，交l1于E，交l4于F，
∵EF⊥l1，l1∥l2∥l3∥l4，
∴EF和l2，l3，l4的夹角都是90°，
即EF与l2，l3，l4都垂直，
∴DE=1，DF=2．
∵四边形ABCD是正方形，
∴∠ADC=90°，AD=CD，
∴∠ADE+∠CDF=90°，
又∵∠α+∠ADE=90°，
∴∠α=∠CDF，
∵... 如图，AB∥CD，AD∥BC，则图中与∠A相等的角有_____个.
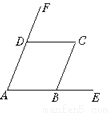
3
【解析】∵AB∥CD，
∴∠A=∠CDF, ∠CBE=∠C;
∵AD∥BC，
∴∠A=∠CBE,
∴∠A=∠CDF=∠CBE=∠C.
∴与∠A相等的角有3个.