题目内容
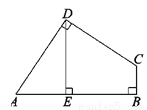
如图，在四边形ABCD中，∠ADC=∠ABC=90°，AD=CD，DE⊥AB于点E，若四边形ABCD的面积为16，则DE=__.
4
【解析】试题解析：过点D作BC的垂线，交BC的延长线于F，
又
∴≌，
∴，
四边形ABCD的面积=正方形DEBF的面积=16，
∴DE=4.
故答案为：4.
如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB=（ ）
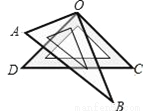
A. 90° B. 120° C. 160° D. 180°
D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°?a，
所以∠AOC+∠BOD=90°+a+90°?a=180°.
故选D. 将表示下列事件发生的概率的字母标在下图中：
（1）投掷一枚骰子，掷出7点的概率
；
（2）在数学测验中做一道四个选项的选择题（单选题），由于不知道那个是正确选项，现任选一个，做对的概率
；
（3）袋子中有两个红球，一个黄球，从袋子中任取一球是红球的概率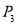
；
（4）太阳每天东升西落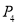
；
（5）在1---100之间，随机抽出一个整数是偶数的概率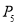
.
【解析】
试题分析：（1）根据骰子没有7点，所以这种情况不可能发生，可知概率为0；
（2）选择题的答案是4选1，因此其概率为；
（3）袋子中摸到红球的概率为；
（4）太阳的东升西落是必然事件，因此其概率为1；
（5）由1---100之间有50个偶数可知随机抽取一个数为偶数的概率为.
试题解析： 下列事件中，属于必然事件的是（ ）
A．随意抛掷一枚骰子，掷得偶数点
B．从一副扑克牌抽出一张，抽得红桃牌
C．任意选择电视的某一频道，正在播放动画片
D．在同一年出生的367名学生中，至少有两个人同月同日生
D
【解析】
试题解析：A、随意抛掷一枚骰子，掷得偶数点是随机事件，故A错误；
B、从一副扑克牌抽出一张，抽得红桃牌是随机事件，故B错误；
C、任意选择电视的某一频道，正在播放动画片是随机事件，故C错误；
D、在同一年出生的367名学生中，至少有两个人同月同日生是必然事件，故D正确；
故选D． 如图，房间内有一架梯子斜靠在墙上，梯子顶端距地面的垂直距离MA为a米，此时梯子的倾斜角为75°，若梯子斜靠在另一面墙时，顶端距地面的垂直距离NB为b米，梯子的倾斜角为45°，则这个房间的宽AB是多少米？为什么？
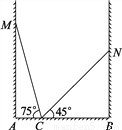
a米．
【解析】试题分析：连结BM、MN，由SSS证明≌，可得∠CBM=∠NBM=45°，AB=AM=a.
试题解析：a米．连结BM、MN，
在△MCN中，∠MCN=180°－75°－45°=60°，CM=CN，
∴△MCN是等边三角形，
∴MC=MN，∠CBN=90°，∠BCN=45°，
∴BC=BN，在△MCB和△MNB中，
∴△MCB≌△MNB，
... 如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（ ）
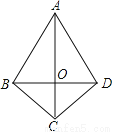
A. 1对 B. 2对 C. 3对 D. 4对
C
【解析】试题分析：在△ABC和△ADC中，根据全等三角形的判定SSS可得△ABC≌△ADC（SSS），根据全等三角形的性质可得∠BAC=∠DAC，∠BCA=∠DCA，在△ABO和△ADO中，可得△ABO≌△ADO（SAS），然后在△BOC和△DOC中，可得△BOC≌△DOC（SAS），
故选：C． 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
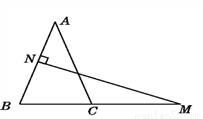
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
(1) 20°；(2) 35°；
(3)规律:∠NMB=∠A.
【解析】（1）根据等边对等角，由AB=AC可得到∠ABM=∠ACB，再结合已知∠A的度数，即可求出∠NMB的度数；
（2）仿照第（1）问的求解过程即可得到∠NMB的度数；
（3）结合上述两问的解答，即可发现∠NMB和∠A之间的大小关系，然后仿照上述解答过程进行验证即可.
【解析】
（1）∵AB=AC，
... 如图，在△ABC中，∠C＝90°，D为BC上一点，且DE⊥AB于E，AC＝AE.求证：AD平分∠BAC.
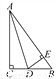
见解析
【解析】试题分析：证明Rt△ACD≌Rt△AED，利用全等三角形的性质即可得.
试题解析：∵DE⊥AB，∴∠AED=90°，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠CAD=∠EAD，
即AD平分∠BAC. 已知：如图，CB⊥AB，CE平分∠BCD，DE平分∠CDA，∠1+∠2=90°，求证：DA⊥AB．
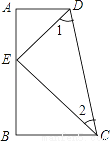
证明见解析.
【解析】试题分析：根据CE平分∠BCD，DE平分∠CDA，得出∠1+∠2=（∠ADC+∠BCD）=90°，∠ADC+∠BCD=180°，证出AD∥BC，再根据CB⊥AB，即可得出DA⊥AB．
【解析】
∵CE平分∠BCD，DE平分∠CDA，
∴∠1=∠ADC，∠2=∠BCD，
∴∠1+∠2=∠ADC+∠BCD=（∠ADC+∠BCD）=90°，
∴∠AD...