题目内容

14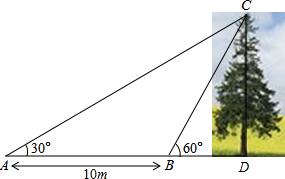．如图，某教学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）则这棵树CD的高度为（　　）
A．10mB．5mC．5$\sqrt{3}$mD．10$\sqrt{3}$m

分析 首先利用三角形的外角的性质求得∠ACB的度数，得到BC的长度，然后在直角△BDC中，利用三角函数即可求解．

解答 解：∵∠CBD=60°，∠CBD=∠A+∠ACB，
∴∠ACB=∠CBD-∠A=60°-30°=30°，
∵∠A=30°，
∴∠A=∠ACB，
∵AB=10，
∴BC=AB=10，
在R△BCD中，CD=BC•sin∠CBD=10×$\frac{\sqrt{3}}{2}$=5$\sqrt{3}$．
故选C．

点评 此题考查了解直角三角形的应用，用到的知识点是三角形的外角、特殊角的三角函数值、等腰三角形的性质，要求学生能借助仰角构造直角三角形并解直角三角形．

练习册系列答案
相关题目
4．计算题
（1）$4\sqrt{5}+\sqrt{45}-\sqrt{8}+4\sqrt{2}$     （2）（$\sqrt{2}-\sqrt{3}$）+2$\sqrt{\frac{1}{3}}$×3$\sqrt{2}$．
5．某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2），经确认扇形图是正确的，而条形图尚有一处错误．
（1）指出条形图中存在的错误，并在原图上改正（涂上阴影）；
（2）在求这20名学生每人植树量的平均数时，小宇是这样分析的：
第一步：此问题中n=4，x1=4，x2=5，x3=6，x4=7；
第二步：求平均数的公式是$\overline{x}$=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{n}$
第三步：$\overline{x}$=$\frac{4+5+6+7}{4}$=5.5
①小宇的分析是从第一步开始出现错误的．
②请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵？
2．如图1，在平面直角坐标系中，直线y=$\frac{3}{4}x-\frac{3}{2}$与抛物线y=-$\frac{1}{4}{x}^{2}+bx+c$交于A、B两点，点A在x轴上，点B的横坐标为-8，与y轴交于点M．
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E．
①如图2，设△PDE的周长为l，点P的横坐标为x，则x的取值范围是-8＜x＜2，求l与x的函数关系式，并求出l的最大值；
②如图3，连接PA，以PA为边作图示一侧的正方形APFG，随着点P的运动，正方形的大小、位置也随之改变，当顶点F或G恰好在y轴上时，直接写出对应的点P的坐标．
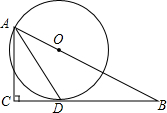9．如图，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D．以AB上一点O为圆心作⊙O，使⊙O经过点A和点D．
（1）求证：直线BC是⊙O的切线；
（2）若AC=3，∠B=30°，求⊙O的半径．
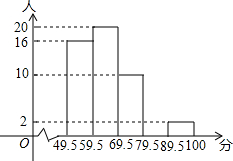19．某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛，为了了解本校初赛的成绩情况，从中抽取了50名学校，将他们的初赛成绩（得分为整数，满分100分）分成五组：
第一组49.5-59.5；第二组59.5-69.5；第三组69.5-79.5；第四组79.5-89.5；第五组89.5-100.5．统计后得到如图所示的频数分布直方图（部分）．观察图形的信息，回答下列问题：
（1）第四组的频数为2（直接写答案）；
（2）若将得分转化为等级，规定：得分低于59.5分评为“D”，59.5-69.5分评分“C”，69.5-89.5分评为“B”，89.5-100.5分评为“A”，那么这200名参加初赛的学生中，参赛成绩评为“D”的学生约有64个（直接填空答案）．
（3）若将抽取出来的50名学生中成绩落在第四、第五组的学生组成一个培训小组，再从这个培训小组中随机挑选2名学生参加决赛，用列表法或画树状图法求：挑选的2名学生的初赛成绩恰好都在90分以上的概率．
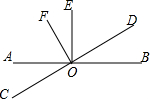6．如图，已知∠AOB、∠COD都为平角，∠AOE、∠BOE、∠COF、∠DOF都等于90°．
（1）写出∠AOF的所有余角；
（2）写出∠BOD的所有补角；
（3）如果∠AOD=4∠EOF，求∠EOF的度数．
3．（1）解方程：x2-3x-4=0；  
（2）解不等式组：$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8＞4x-1}\end{array}\right.$．
4．正六边形的周长为12，则该正六边形的内切圆的半径为（　　）
A．1B．$\sqrt{3}$C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网