题目内容
9.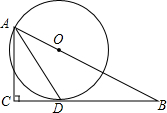 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)求证:直线BC是⊙O的切线;
(2)若AC=3,∠B=30°,求⊙O的半径.
分析 (1)连接OD,根据角平分线的定义和等腰三角形的性质证明OD∥AC,根据平行线的性质得到∠C=90°,根据切线的判定定理证明;
(2)过点O作OM⊥AD垂足为M,根据垂径定理和余弦的概念计算即可.
解答 (1)证明:连接OD,则OA=OD,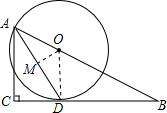
∴∠OAD=ODA,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴直线BC是⊙O的切线;
(2)解:∵∠B=30°,
∴∠BAC=60°,
∵AD平分∠BAC,
∴∠CAD=∠BAD=30°,
∴AD=AC÷cos30°=2$\sqrt{3}$,
过点O作OM⊥AD垂足为M,则AM=$\frac{1}{2}$AD=$\sqrt{3}$,
OA=AM÷cos30°=2,
∴⊙O的半经为2.
点评 本题考查的是切线的判定定理、垂径定理、锐角三角函数的概念,掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
20. 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
4.下列图形中,既是中心对称图形,又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.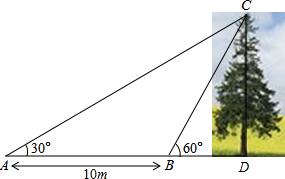 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
1.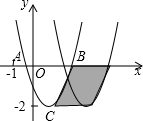 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )| A. | b>0 | B. | a-b+c<0 | ||
| C. | 阴影部分的面积为4 | D. | 若c=1,则b2=-4a |
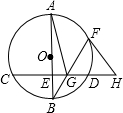 如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.
如图.AB为⊙O的直径,CD为⊙O的弦,且AB⊥CD于E,F为劣弧AD上一点,BF交CD于点C,过点F作⊙O的切线,交CD的延长线于H.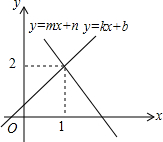 如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.