题目内容
4.正六边形的周长为12,则该正六边形的内切圆的半径为( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 根据题意画出图形,利用正六边形中的等边三角形的性质和三角函数求解即可.
解答 解:如图,连接OA、OB,OG;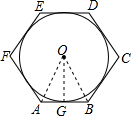
∵六边形ABCDEF的周长为12,
∴AB=2,∠AOB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2,
∴OG=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故选:B.
点评 此题主要考查正多边形的性质、三角函数、等边三角形的判定与性质,属于常规题,正多边形的计算常用的方法是转化为直角三角形或等腰三角形的计算.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
14.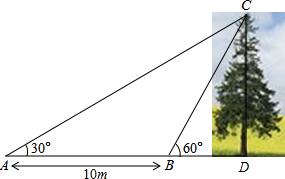 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
15.下列命题不正确的是( )
| A. | 所有等腰直角三角形都相似 | |
| B. | 两边对应相等的两个直角三角形全等 | |
| C. | 圆中垂直于弦的直径平分这条弦 | |
| D. | 顺次连接对角线相等的四边形各边中点得到的四边形是矩形 |
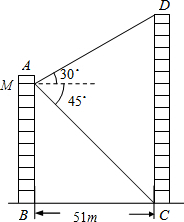 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)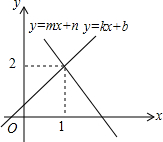 如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$. 如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.
如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.