题目内容
5.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.(1)指出条形图中存在的错误,并在原图上改正(涂上阴影);
(2)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:此问题中n=4,x1=4,x2=5,x3=6,x4=7;
第二步:求平均数的公式是$\overline{x}$=$\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{n}$
第三步:$\overline{x}$=$\frac{4+5+6+7}{4}$=5.5
①小宇的分析是从第一步开始出现错误的.
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵?

分析 (1)条形统计图中D的人数错误,应为20×10%;
(2)①小宇的分析是从第一步开始出现错误的;
②求出正确的平均数,乘以260即可得到结果.
解答 解:(1)条线统计图中D类型为3人错了.应该是20×10%=2(人); 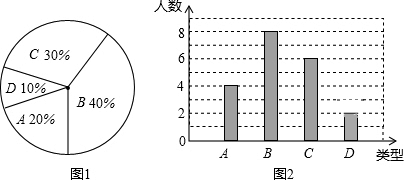
(2)①第一步;
②正确的平均数是:$\overline{x}$=$\frac{4×4+5×8+6×6+7×2}{20}$=5.3(棵).
答:估计260名学生共植树5.3×260=1378(棵).
点评 此题考查了条形统计图,扇形统计图,加权平均数,以及用样本估计总体,弄清题意从统计图中找出数据以及计算方法是解本题的关键.

练习册系列答案
相关题目
20. 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
 如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
如图,AB为半圆的直径,其AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
14.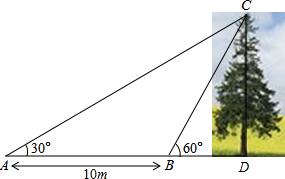 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
15.下列命题不正确的是( )
| A. | 所有等腰直角三角形都相似 | |
| B. | 两边对应相等的两个直角三角形全等 | |
| C. | 圆中垂直于弦的直径平分这条弦 | |
| D. | 顺次连接对角线相等的四边形各边中点得到的四边形是矩形 |
 如图,将矩形ABCD沿EF折叠,C点落在C′,D点落在D′处,ED′的延长线交BC于点G,若∠EFG=68°,求∠1、∠2的度数.
如图,将矩形ABCD沿EF折叠,C点落在C′,D点落在D′处,ED′的延长线交BC于点G,若∠EFG=68°,求∠1、∠2的度数.