题目内容
3.(1)解方程:x2-3x-4=0;(2)解不等式组:$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8>4x-1}\end{array}\right.$.
分析 (1)将方程左边因式分解化为两个一元一次方程求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)将方程左边因式分解,得:(x+1)(x-4)=0,
所以x+1=0或x-4=0,
解得:x1=4,x2=-1;
(2)解不等式x-1≥1-x,得:x≥1,
解不等式x+8>4x-1,得:x<3,
故不等式组的解集为:1≤x<3.
点评 本题考查的是解一元一次不等式组和解一元二次方程的基本技能,熟练掌握解方程的基本方法和正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.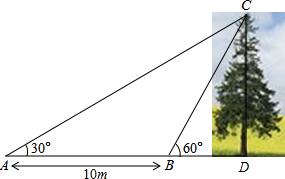 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
8.用换元法解方程:$\frac{{x}^{2}-2}{x}$+$\frac{2x}{{x}^{2}-2}$=3时,若设$\frac{{x}^{2}-2}{x}=y$,并将原方程化为关于y的整式方程,那么这个整式方程是( )
| A. | y2-3y+2=0 | B. | y2-3y-2=0 | C. | y2+3y+2=0 | D. | y2+3y-2=0 |
15.下列命题不正确的是( )
| A. | 所有等腰直角三角形都相似 | |
| B. | 两边对应相等的两个直角三角形全等 | |
| C. | 圆中垂直于弦的直径平分这条弦 | |
| D. | 顺次连接对角线相等的四边形各边中点得到的四边形是矩形 |
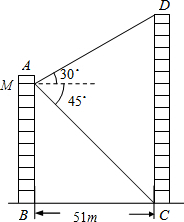 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)