题目内容
19.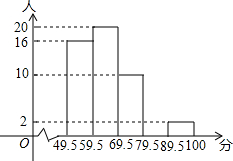 某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:
某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:第一组49.5-59.5;第二组59.5-69.5;第三组69.5-79.5;第四组79.5-89.5;第五组89.5-100.5.统计后得到如图所示的频数分布直方图(部分).观察图形的信息,回答下列问题:
(1)第四组的频数为2(直接写答案);
(2)若将得分转化为等级,规定:得分低于59.5分评为“D”,59.5-69.5分评分“C”,69.5-89.5分评为“B”,89.5-100.5分评为“A”,那么这200名参加初赛的学生中,参赛成绩评为“D”的学生约有64个(直接填空答案).
(3)若将抽取出来的50名学生中成绩落在第四、第五组的学生组成一个培训小组,再从这个培训小组中随机挑选2名学生参加决赛,用列表法或画树状图法求:挑选的2名学生的初赛成绩恰好都在90分以上的概率.
分析 (1)由抽取了50名学生,结合直方图,即可求得第四组的频数;
(2)利用样本即可估算总体,即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与挑选的2名学生的初赛成绩恰好都在90分以上的情况,再利用概率公式即可求得答案.
解答 解:(1)第四组的频数为:50-16-20-10-2=2,
故答案为:2;
(2)参赛成绩评为“D”的学生约有:200×$\frac{16}{50}$=64(个);
故答案为:64;
(3)画树状图得: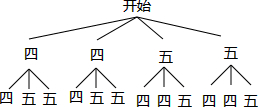
∵共有12种等可能的结果,挑选的2名学生的初赛成绩恰好都在90分以上的有2种情况,
∴挑选的2名学生的初赛成绩恰好都在90分以上的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了列表法或树状图法求概率以及直方图的知识.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
14.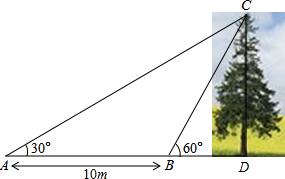 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
8.用换元法解方程:$\frac{{x}^{2}-2}{x}$+$\frac{2x}{{x}^{2}-2}$=3时,若设$\frac{{x}^{2}-2}{x}=y$,并将原方程化为关于y的整式方程,那么这个整式方程是( )
| A. | y2-3y+2=0 | B. | y2-3y-2=0 | C. | y2+3y+2=0 | D. | y2+3y-2=0 |
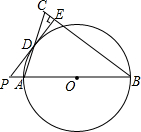 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P. 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).