题目内容
2.为了让老师和学生有一个更加舒适的教学环境,重庆一中决定为教学楼更换空调.已知甲安装队为南楼安装55台空调,乙安装队为北楼安装50台空调,两队同时开工,恰好同时完成任务,甲队比乙队每天多安装两台,求甲、乙两队每天安装的台数分别是多少?分析 设乙队每天安装x台,则甲队每天安装(x+2)台,根据两队同时开工,恰好同时完成任务,即所用的时间相等,即可列方程求解.
解答 解:设乙队每天安装x台,则甲队每天安装(x+2)台.
由题意得:$\frac{55}{x+2}=\frac{50}{x}$,
解得:x=20.
经检验:x=20是原方程的根,
则x+2=22.
答:甲队每天安装22台,乙队每天安装20台.
点评 本题考查了分式方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
12.将抛物线y=x2+5向右平移1个单位长度,再向下平移2个单位长度,后,得到的抛物线解析式是( )
| A. | y=(x-1)2+3 | B. | y=(x+1)2+3 | C. | y=(x+1)2-3 | D. | y=(x-1)2-3 |
17.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
| A. | 11 | B. | 14 | C. | 19 | D. | 14或19 |
14.下列计算中正确的是( )
| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
 如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.
如图,在正方形ABCD中,AC与BD相交于点O,E为AD上的一点,连接BE,点G在BE上,连结OG并延长交AD于点F,若∠FGE=45°.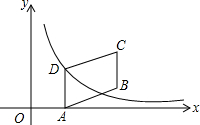 如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.
如图,四边形ABCD是平行四边形,点A(1,0)、B(3,1)、C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,则m=2.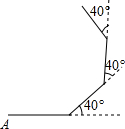 如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.
如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.