题目内容
7．在等式$\frac{1}{F}=\frac{1}{f_1}+\frac{2}{f_2}$中，f2≠2F，则f1=$\frac{{f}_{2}F}{{f}_{2}-2F}$（用F、f2的式子表示）分析 等式变形后，通分并利用同分母分式的加法法则变形，即可表示出f1．
解答 解：等式$\frac{1}{F}=\frac{1}{f_1}+\frac{2}{f_2}$，
变形得：$\frac{1}{{f}_{1}}$=$\frac{1}{F}$-$\frac{2}{{f}_{2}}$=$\frac{{f}_{2}-2F}{{f}_{2}F}$，
则f1=$\frac{{f}_{2}F}{{f}_{2}-2F}$．
故答案为$\frac{{f}_{2}F}{{f}_{2}-2F}$．
点评 本题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，木工师傅用角尺画出工件边缘的两条垂线，这两条垂线平行吗？为什么？
16．下列方程中，有实数根的是（ ）
| A． | x2-3x+5=0 | B． | $\sqrt{x-2}+1=0$ | C． | $\sqrt{x+2}=-x$ | D． | $\frac{x}{{{x^2}-1}}=\frac{1}{{{x^2}-1}}$ |
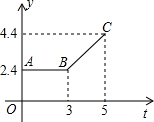如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．