题目内容
12.你能化简(x-1)(x99+x98+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,然后归纳出一些方法,分别化简下列各式并填空:(x-1)(x+1)=x2-1;(x-1)(x2+x+1)=x3-1;(x-1)(x3+x2+x+1)=x4-1…根据上述规律,可得(x-1)(x99+x98+…+x+1)=x100-1
请你利用上面的结论,完成下面问题:
计算:299+298+297+…+2+1,并判断末位数字是几.
分析 根据平方差公式,和立方差公式可得前2个式子的结果,利用多项式乘以多项式的方法可得出第3个式子的结果;从而总结出规律是(x-1)(x99+x98+x97+…+x+1)=x100-1,根据上述结论计算下列式子即可.
解答 解:根据题意:(1)(x-1)(x+1)=x2-1;
(2)(x-1)(x2+x+1)=x3-1;
(3)(x-1)(x3+x2+x+1)=x4-1,
故(x-1)(x99+x98+x97+…+x+1)=x100-1
故答案为:x100-1;
根据以上分析:
299+298+297+…+2+1=(2-1)(299+298+297+…+2+1)=2100-1;
末位数字是5.
点评 本题主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
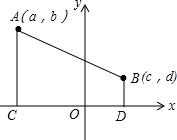 已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D. 如图,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=56°,则∠2-∠1=44°.
如图,将一张长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置上,ED′的延长线与BC的交点为G,若∠EFG=56°,则∠2-∠1=44°.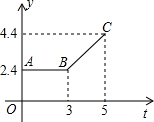 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.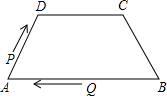 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.