题目内容
14.下列计算中正确的是( )| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
分析 根据二次根式的性质对A、D进行判断;根据最简二次根式的定义对B进行判断;根据二次根式的乘法法则对C进行判断.
解答 解:A、原式=|m|+|n|,所以A选项错误;
B、$\sqrt{{a}^{2}-{b}^{2}}$为最简二次根式,所以B选项错误;
C、原式=$\sqrt{3×2}$=$\sqrt{6}$,所以C选项正确;
D、原式=|-3|=3,所以D选项错误.
故选C.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
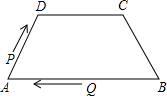 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.