题目内容
15. 如图:已知△ABC∽△ADE,AD=9cm,AE=12cm,AB=4cm,则CE=$\frac{20}{3}$ cm.
如图:已知△ABC∽△ADE,AD=9cm,AE=12cm,AB=4cm,则CE=$\frac{20}{3}$ cm.
分析 由相似三角形的性质:对应边的比值性质可求出AC的长,再由CE=AE-AC即可求出CE的长.
解答 解:∵△ABC∽△ADE,
∴AB:AD=AC:AE,
∵AD=9cm,AE=12cm,AB=4cm,
∴4:9=AC:12,
∴AC=$\frac{16}{3}$,
∴CE=AE-AC=$\frac{20}{3}$cm,
故答案为$\frac{20}{3}$.
点评 本题主要考查相似三角形的性质,掌握相似三角形的对应边成比例是解题的关键.

练习册系列答案
相关题目
6.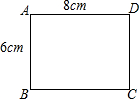 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
 在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )
在一张长为8cm,宽为6cm的矩形纸片上,要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的顶点A重合,其余的两个顶点都在矩形的边上).这个等腰三角形有几种剪法?( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.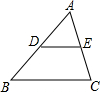 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
20.a为任意实数时,下列分式一定有意义的是( )
| A. | $\frac{{{a^2}+a}}{a}$ | B. | $\frac{a}{{{a^2}+1}}$ | C. | $\frac{a}{{{a^2}-1}}$ | D. | $\frac{1}{{{a^2}-1}}$ |
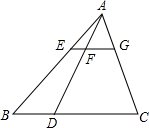 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.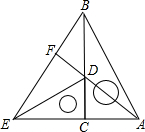 把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.试说明:
把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE,AD,AD的延长线交BE于点F.试说明: