题目内容
5.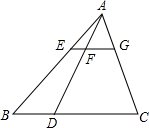 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.(1)求证:AE:AF:AG=BE:DF:CG;
(2)若AD是中线,求证:EF=GF.
分析 (1)由EG∥BC可知$\frac{AE}{BE}=\frac{AF}{DF}=\frac{AG}{GC}$,由比例的性质可知:AE:AF:AG=BE:DF:CG;
(2)根据已知条件得到△AEF∽△ABD,△AFG∽△ADC,推出$\frac{EF}{BD}=\frac{FG}{DC}$,根据BD=CD即可得到结论.
解答 证明:(1)∵EG∥BC,
∴$\frac{AE}{BE}=\frac{AF}{DF}=\frac{AG}{GC}$.
∴AE:AF:AG=BE:DF:CG.
(2)∵EF∥BC,
∴△AEF∽△ABD,△AFG∽△ADC.
∴$\frac{EF}{BD}=\frac{AF}{AD}$,$\frac{FG}{DC}=\frac{AF}{AD}$.
∴$\frac{EF}{BD}=\frac{FG}{DC}$.
∵AD为△ABC的边BC上的中线,
∴BD=CD.
∴GF=GE.
点评 本题考查了相似三角形的性质和判定、平行线分线段成比例定理、比例的性质,证得$\frac{EF}{BD}=\frac{FG}{DC}$是解题的关键.

练习册系列答案
相关题目
10.如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1面积为S1,△B3D2C2面积为S2,…,△Bn+1DnCn面积为Sn,则S2013等于( )


| A. | $\frac{2013}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2013\sqrt{3}}{2014}$ | D. | $\frac{2014\sqrt{3}}{2015}$ |
 如图,已知⊙O的半径为3,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCPE是平行四边形,则AD的长为6.
如图,已知⊙O的半径为3,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCPE是平行四边形,则AD的长为6.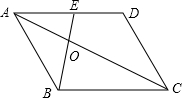 如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.
如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.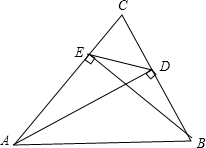 如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.
如图,AD,BE是△ABC的两条高,求证:∠CED=∠ABC.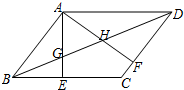 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF分别相交于GH. 如图:已知△ABC∽△ADE,AD=9cm,AE=12cm,AB=4cm,则CE=$\frac{20}{3}$ cm.
如图:已知△ABC∽△ADE,AD=9cm,AE=12cm,AB=4cm,则CE=$\frac{20}{3}$ cm.