题目内容
7．湖口县金沙湾九江钢铁厂，在去年取得22亿元利润的优异成绩下，今年决定再招聘甲乙两个工种的工人共300人，甲、乙两个工种的工人工资分别为每月1200元和2000元，现要求乙种工人的人数不少于甲种工人人数的2倍，那么招聘甲种工人多少人时，可使每月所付工资最少？分析 设招聘甲种工人x人，则乙种工人为（300-x）人，根据乙种工人的人数不少于甲种工人人数的2倍，可得不等式．
解答 解：设招聘甲种工人x人，则乙种工人为（300-x）人，
依题意得300-x≥2x，
解得：x≤100，
∵甲、乙两个工种的工人工资分别为每月1200元和2000元，
∴应尽可能多的招聘甲种工人．
故应招聘甲种工人100人．
答：招聘甲种工人100人时，可使每月所付工资最少．
点评 本题考查了一元一次不等式的应用，解答本题的关键是仔细审题，找到不等关系，难度一般．
练习册系列答案
相关题目
如图，已知AD、BC相交于点O，OA=OC，OB=OD．求证：∠A=∠C．
如图：已知△ABC∽△ADE，AD=9cm，AE=12cm，AB=4cm，则CE=$\frac{20}{3}$ cm．
2．
如图，点C是线段AB的黄金分割点，则下列各式正确的是（ ）
如图，点C是线段AB的黄金分割点，则下列各式正确的是（ ）| A． | $\frac{AC}{BC}=\frac{AB}{AC}$ | B． | $\frac{BC}{AB}=\frac{AC}{BC}$ | C． | $\frac{AC}{AB}=\frac{AB}{BC}$ | D． | $\frac{BC}{AB}=\frac{AC}{AB}$ |
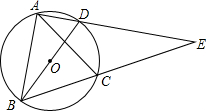如图，BD是⊙O的直径，A、C是⊙O上的两点，且AB=AC，AD与BC的延长线交于点E．
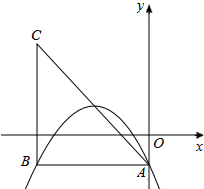在平面直角坐标系中，已知抛物线y=ax2-2x+c（a，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，-1），C的坐标为（-4，3），直角顶点B在第二象限．