题目内容
7.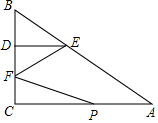 如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.(1)线段AC的长=6;
(2)当△PCF与△EDF相似时,求t的值.
分析 (1)作EH⊥AC于H,如图,易得四边形CDEH为矩形,从而得到CH=DE=2,EH=CD=3,然后利用勾股定理计算出AH即可得到AC的长;
(2)CF=t,PA=2t,则DF=3-t,CP=6-2t,0<t<3,由于∠C=∠FDE,根据两组对应边的比相等且夹角对应相等的两个三角形相似可分类讨论:若$\frac{CF}{DF}$=$\frac{CP}{DE}$时,△CFP∽△DFE,若$\frac{CF}{DE}$=$\frac{CP}{DE}$,则△CFP∽△DEF,然后分别利用相似比得到关于t的方程,再解方程求出t即可.
解答 解:(1)作EH⊥AC于H,如图,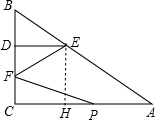 ∵∠C=90°,DE∥AC,
∵∠C=90°,DE∥AC,
∴四边形CDEH为矩形,
∴CH=DE=2,EH=CD=3,
在Rt△AEH中,AH=$\sqrt{A{E}^{2}-E{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AC=CH+AH=2+4=6;
(2)CF=t,PA=2t,则DF=3-t,CP=6-2t,0<t<3,
∵∠C=∠FDE,
∴当$\frac{CF}{DF}$=$\frac{CP}{DE}$时,△CFP∽△DFE,即$\frac{t}{3-t}$=$\frac{6-2t}{2}$,整理得t2-7t+9=0,解得t1=$\frac{7-\sqrt{13}}{2}$,t2=$\frac{7+\sqrt{13}}{2}$(舍去),
∴当$\frac{CF}{DE}$=$\frac{CP}{DE}$时,△CFP∽△DEF,即$\frac{t}{2}$=$\frac{6-2t}{3-t}$,t=4(舍去),
综上所述,t的值为$\frac{7-\sqrt{13}}{2}$.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了勾股定理.

 阅读快车系列答案
阅读快车系列答案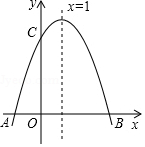 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,交y轴于C点,其中B点坐标为(3,0),C点坐标为(0,3),且图象对称轴为直线x=1.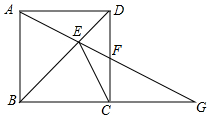 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.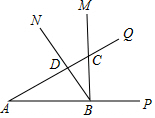 如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )
如图,∠PAQ=∠MBN=30°,∠MBN的顶点B在射线AP上,射线BM和射线BN分别交射线AQ于点C、D,当∠MBN绕点B转动时.若AB=2$\sqrt{3}$,则CA•CD的最小值是( )