题目内容
16.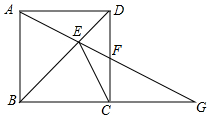 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.
如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F,求证:CE与△CFG的外接圆相切.点拨:此题图上没有画出△CFG的外接圆,但△CFG是直角三角形,圆心在斜边FG的中点,为此我们取FG的中点O,连结OC,证明CE⊥OC即可得解.
分析 取FG的中点O,连结OC,证明△ADE≌△CDE,得到∠DAE=∠DCE,根据平行线的性质得到∠DAE=∠G,得到∠G=∠DCE,根据直角三角形的性质得到∠OCE=90°,根据切线的判定定理证明结论.
解答 证明:取FG的中点O,连结OC,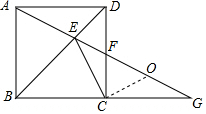
∵四边形ABCD是矩正方形,
∴AD=DC,∠ADB=∠CDB,
在△ADE和△CDE中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△ADE≌△CDE,
∴∠DAE=∠DCE,
∵AD∥BG,
∴∠DAE=∠G,
∴∠G=∠DCE
∵O为FG的中点,
∴OF=OC,
∴∠OFC=∠OCF,
∵∠G+∠OFC=90°,
∴∠DCE+∠OCF=90°,即∠OCE=90°,
∴CE与△CFG的外接圆相切.
点评 本题考查的是圆的切线的判定、正方形的性质、全等三角形的判定与性质、等腰三角形的性质、直角三角形的性质,掌握圆的切线的判定定理、直角三角形斜边上的中线是斜边的一半是解题的关键.

练习册系列答案
相关题目
7.已知一组数据:7,5,9,5,14,下列说法不正确的是( )
| A. | 平均数是8 | B. | 极差是9 | C. | 众数是5 | D. | 中位数是9 |
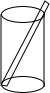 一种乘饮料的圆柱形杯子,测得内部底面半径为2.5cm,高为12cm,吸管最放进杯里(如图),杯口外面露出部分的吸管长为4.6cm,问吸管为多长?
一种乘饮料的圆柱形杯子,测得内部底面半径为2.5cm,高为12cm,吸管最放进杯里(如图),杯口外面露出部分的吸管长为4.6cm,问吸管为多长? 如图,在?ABCD中,对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM=DN且BA∥DN.
如图,在?ABCD中,对角线AC、BD相交于点O,M、N分别是OA、OC的中点,求证:BM=DN且BA∥DN.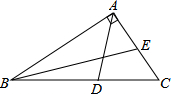 如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论:
如图,在△ABC中,∠BAC=90°,AD是角平分线,BE是中线,则下列结论: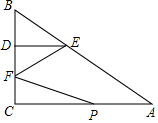 如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.
如图,在Rt△ABC中,∠C=90°,点D在BC上,点E在AB上,且DE∥AC,AE=5,DE=2,DC=3,动点P从点A出发,沿边AC以每秒2个单位长的速度向终点C运动,同时动点F从点C出发,在线段CD上以每秒1个单位长的速度向终点D运动,设运动时间为t秒.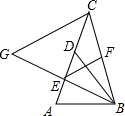 在△ABC中,点D在边AC上,BD=BA,点E是AD的中点,点F是BC的中点.
在△ABC中,点D在边AC上,BD=BA,点E是AD的中点,点F是BC的中点.