题目内容
19.计算:(1)(x+y)(x2-xy+y2)
(2)-12x2y•($\frac{1}{3}$x3y2-$\frac{3}{4}{x}^{2}y$+$\frac{1}{6}$)
分析 (1)根据多项式与多项式相乘的法则和合并同类项法则计算即可;
(2)根据单项式与多项式相乘的法则以及合并同类项法则计算即可.
解答 解:(1)原式=x3-x2y+xy2+x2y-xy2+y3
=x3+y3;
(2)原式=-12x2y•$\frac{1}{3}$x3y2+12x2y•$\frac{3}{4}$x2y-12x2y•$\frac{1}{6}$
=-4x5y3+9x4y2-2x2y.
点评 本题考查的是多项式乘多项式,掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加是解题的关键.

练习册系列答案
相关题目
4.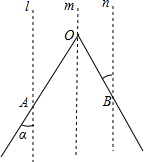 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
 如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )
如图,已知:∠AOB=60°,点A、B分别在∠AOB两边上,直线l、m、n分别过A、O、B三点,且满足直线l∥m∥n,OB与直线n所夹的角为25°,则∠α的度数为( )| A. | 25° | B. | 45° | C. | 35° | D. | 30° |
9.下列根式中,最简二次根式是( )
| A. | $\sqrt{{m}^{2}+{n}^{2}}$ | B. | $\sqrt{16m}$ | C. | $\sqrt{\frac{m}{2}}$ | D. | $\sqrt{0.5}$ |
 如图,a∥b,∠1=76°,∠3=72°,则∠2的度数是32°.
如图,a∥b,∠1=76°,∠3=72°,则∠2的度数是32°.